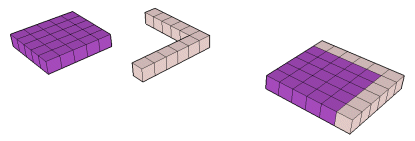
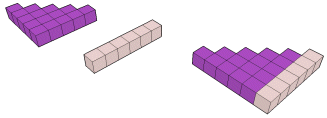
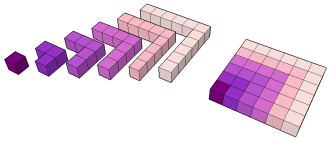Parte 2 : quadrados e triângulos
Números quadrados (o primeiro e os outros)
Definição { quadrado }:
A unidade é o primeiro quadrado;
A soma de um quadrado com o ímpar de ordem seguinte é um quadrado.
Notação { quadrado de ordem n, n2 }:
12 := 1
(n+1)2 := n2 + in+1
Propriedade:
O quadrado de ordem n é a soma dos n primeiros ímpares.
Notação:
n2 = i1 + i2 + ... + in
Porque:
O primeiro quadrado é o primeiro ímpar;
O quadrado de ordem n+1 é a soma dos n primeiros ímpares,
somada com o ímpar de ordem n+1.
| |
52 = i1 + i2 + i3 + i4 + i5
62 = i1 + i2 + i3 + i4 + i5 + i6
|
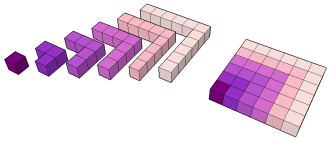
|
Portanto:
A diferença de dois quadrados é uma soma de ímpares consecutivos.
Notação:
m2 - n2 = in+1 + in+2 + ... + im
| |
102 - 62 = i7 + i8 + i9 + i10
|
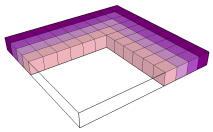
|
Portanto:
(m+n)2 - n2 = in+1 + in+2 + ... + im+n
| |
(4+6)2 - 62 = i6+1 + i6+2 + i6+3 + i6+4
|

|
Portanto:
(m+n)2 - n2 = 2 x m x n + m2
Porque:
in+k = in + ik + 1
(m+n)2 - n2 = m (in + 1) + i1 + i2 + ... + im = m x 2 x n + m2
| |
(4+6)2 - 62 = 2 x 4 x 6 + 42
|
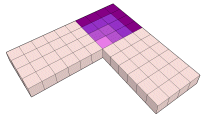
|
Portanto:
(m+n)2 - n2 - m2 = 2 x m x n
| |
(4+6)2 - 62 - 42 = 2 x 4 x 6
|
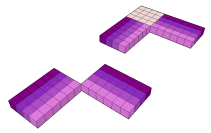
|
Portanto:
(m+n)2 = m2 + n2 + 2 x m x n
| |
(4+6)2 = 42 + 62 + 2 x 4 x 6
|

|
Propriedade:
O quadrado de ordem n é n vezes o número n.
Notação:
n2 = n x n
Porque:
O primeiro quadrado é o primeiro número;
O quadrado de ordem n+1 é obtido a partir do quadrado de ordem n,
somando n vezes a unidade com o número n+1.
| |
52 = 5 x 5
62 = 52 + i6 = 52 + 5 + 6
|
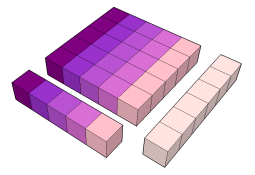
|
Propriedade:
Um quadrado de ordem ímpar é um ímpar (de ordem ímpar);
um quadrado de ordem par é um par (de ordem par).
Notação:
in2 = i2 n (n-1) + 1
(2 n)2 = n x 2 x 2 n = 4 x n2
| |
52 = i32 = i13
|
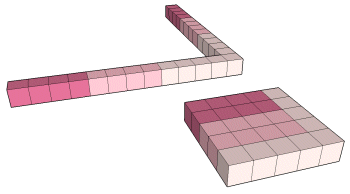
|
| |
62 = (2 x 3)2 = 3 x 2 x 6
= 4 x 32
|
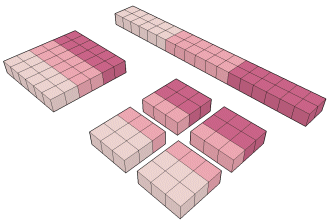
|
Números triangulares (o primeiro e os outros)
Definição { triângulo }:
A unidade é o primeiro triângulo;
A soma de um triângulo com o número seguinte é um triângulo.
Notação { triângulo de ordem n, tn }:
t1 := 1
tn+1 := tn + n+1
Propriedade:
O triângulo de ordem n é a soma dos n primeiros números.
Notação:
tn = 1 + 2 + 3 + ... + n
Porque:
O primeiro triângulo é o primeiro número;
O triângulo de ordem n+1 é a soma dos n primeiros números,
somada com n+1.
| |
t5 = 1 + 2 + 3 + 4 + 5
t6 = 1 + 2 + 3 + 4 + 5 + 6
|
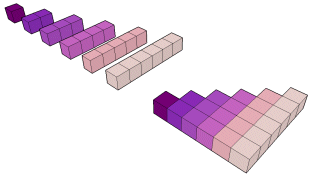
|
Propriedade:
A soma de dois triângulos consecutivos é um quadrado.
Notação:
tn + tn+1 = (n+1)2
Porque:
A soma dos dois primeiros triângulos é o segundo quadrado;
Para passar à soma seguinte de triângulos consecutivos, é necessário somar
dois números consecutivos, ou seja, o ímpar seguinte.
| |
t4 + t5 = 52
t5 + t6 = 52 + 5 + 6 = 62
|
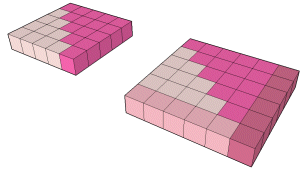
|
Portanto:
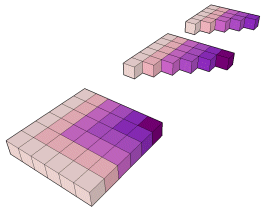
A soma dos n primeiros números, mais a soma dos n+1 primeiros números,
é a soma dos n+1 primeiros ímpares.
| |
t5 = 1 + 2 + 3 + 4 + 5
t6 = 1 + 2 + 3 + 4 + 5 + 6
62 = i1 + i2 + i3 + i4 + i5 + i6
|
|
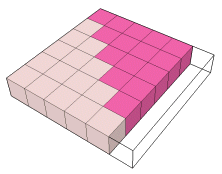
Portanto:
A soma de dois triângulos iguais não é um quadrado.
| |
t5 + t5 + 6 = 62
|
|
para outras partes:
(anterior)
1
2
3
4
5
6
(próxima)
{ Rosália Rodrigues, 2006 }