Quantum Transport@I3N

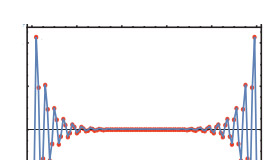
Flat bands in the one-particle tight-binding energy dispersion of geometrically frustrated lattices reflect the existence of degenerate localized eigenstates which are translated versions of the same state $\vert \psi_{loc}\rangle $. The probability density associated with one of these localized states is non-zero only in a small lattice region. In the particular case of decorated lattices of the Lieb’s class, the localized states can be viewed as one-dimensional standing waves in tight-binding rings, associated with paths in the 2D lattice which include one or two plaquettes.

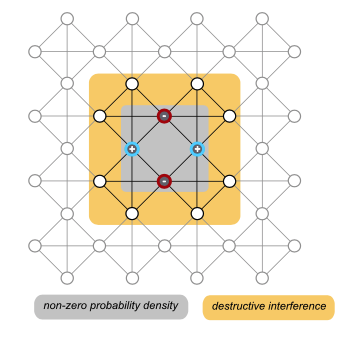
Localized states in the Mielke lattice

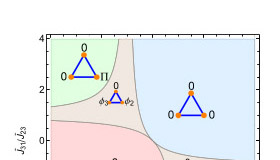
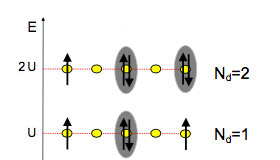
The multiband scenario has been considered to describe many supercondutors, in particular iron-based superconductors. Recently we have discussed frustration effects in a clean multiband superconductor induced by repulsive interband interactions. We have shown that these frustration effects lead to one or several phase transitions with increasing temperature from or to chiral superconducting states with broken time-reversal symmetry with continuous evolution of the relative phases of the superconducting order parameters. These transitions are signaled by slope changes in the temperature dependence of the superconducting gaps. In the case of quasi-2D superconductors, such transitions also occur with increasing in-plane magnetic field.

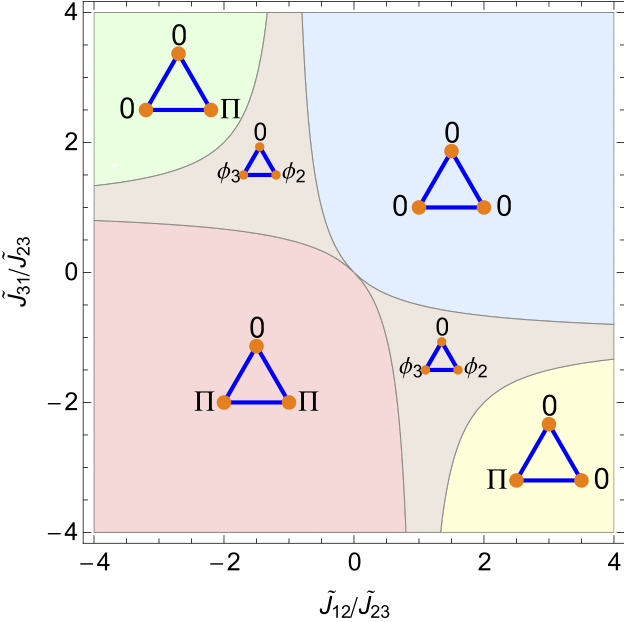
Phase diagram of frustrated three-band superconductor

Restricting the $n$-band superconducting system to the subspace constructed from the usual set of BCS states, with superconducting gaps $\Delta=(\Delta_1,\cdots,\Delta_n)$ and respective phases, $ \Phi=(\phi_1,\cdots,\phi_n)$, the eigenvalues of the Hamiltonian in this basis are \begin{eqnarray} E &=& \sum_i f_i(\left\vert \Psi_{i} \right\vert^{2}) - \sum_i V_{ii} \left\vert \Psi_{i} \right\vert^{2} \nonumber \\ &-& \sum_{i \neq j} V_{i,j} \left\vert \Psi_{i} \right\vert \left\vert \Psi_{j} \right\vert \cos(\phi_{j}-\phi_{i}), \label{eq:zeroTenergy} \end{eqnarray} where $f_i(\left\vert \Psi_{i} \right\vert^{2})$ is the kinetic energy contribution. This should be compared with the energy of a system of $n$ two-component classical spins (written as $\vec{S}_i= S_i (\cos \phi_i, \sin \phi_i)$), governed by the Heisenberg Hamiltonian $H=\sum_{i>j} J_{ij} \vec{S}_i \cdot \vec{S}_j$. The energy of this system for a given set of magnitudes $\{S_i \}$ and angles $\{\phi_i \}$ is $E_J(\{ \phi_i \})=\sum_{i>j} J_{ij} S_i S_j \cos (\phi_i-\phi_j)=\sum_{i>j} \tilde{J}_{ij} \cos (\phi_i-\phi_j)$ where $\tilde{J}_{ij}=J_{ij} S_i S_j$.

The minimization of the free energy with respect to the phases $\phi_{i}$ gives \begin{equation} \hspace{-1cm} \sum_j V_{i,j} \left\vert \Psi_{j} \right\vert \sin (\phi_{j}-\phi_{i}) = 0, \, \forall i. \end{equation} and with respect to the absolute values of the superconducting parameters, \begin{equation} \Delta_i = \sum_{j} V_{ij} \cos(\Delta\phi_{ij}) \int_0^{\omega_D} d\xi_j K_j(\xi_j,\Delta_j,T) \Delta_j , \label{eq:gapequation1} \end{equation} where $ K_j(\xi,\Delta,T)={N_j(\xi) \over E} \tanh {E \over 2t} , $, \\ $ E=\sqrt{\xi^2+\Delta^2}$, $\omega_D$ is the usual frequency cutoff, $N_j(\xi)$ is the density of states of the $j$ band and $t=k_B T$.

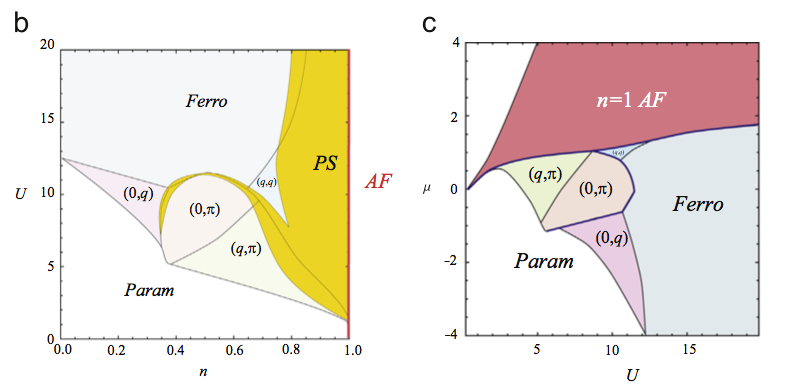
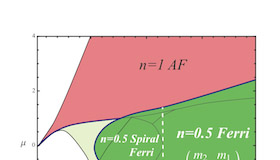
(n,U) and (U,$\mu$) mean-field phase diagrams for the 2D Hubbard model, allowing for phase separation

The ground state magnetic phase diagram of interacting electronic models is still an open problem in condensed matter physics, despite multiple theoretical and computational efforts during the last decades. In fact, even at the mean-field (MF) level, depending on the magnetic phases allowed, different authors obtain different diagrams for example in the case of the Hubbard model on the square lattice. The traditional orderings are ferromagnetism, anti-ferromagnetism and paramagnetism, but other phases may be considered such as spin spiral phases or spatial phase separation.

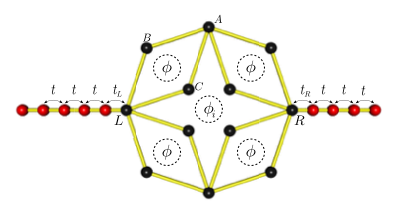
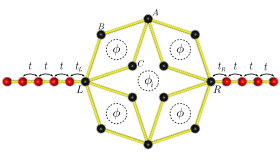
Cluster connected to 1D leads

Conductance calculations are based on the Meir–Wingreen formulation (which is based on the non- equilibrium Green’s functions method and takes into account electronic interactions in the cluster) or on the traditional quantum scattering approach (which is a one-particle description of scattering events due to potential barriers). The quantum scattering description of the transmission of a 1D particle across a structural or potential barrier is closely analogous to the Fresnel description of a plane light wave incident in a interface between two dielectric media. The wavefunction of a particle with momentum $k$ and energy $\epsilon_k$ is written as an incident wave plus reflected and transmitted waves with amplitudes $r(\epsilon_k)$ and $t(\epsilon_k)$ respectively, relatively to the incident wave. The transmission probability for this incident wave is $\vert t(\epsilon_k) \vert^2$.

The linear conductance $G(T)$ of non-interacting fermions is determined using the Landauer formula, which relates the transmission probability $|t(\epsilon)|^2 $ with the linear conductance $G(T)$ of the non-interacting fermions at temperature $T$. This formula is explained in the following way. A single state with a momentum $k$ (and an energy $\epsilon_k=-2 \cos k$ of the band of a 1D lead) carries a current $ev_k/L $ where $v_k$ is the 1D velocity of the electron, $\hbar v_k=\partial \epsilon_k /\partial k$ and $L$ is the length of the lead. The contribution to the current of the positive velocity states in an interval $\Delta k$ is therefore $I_{\Delta k} =e/(\hbar L) \sum_{k \, \Delta k} d \epsilon_k /d k$. Assuming $L$ very large, so that the $k$ values are effectively continuous, the summation over $k$ can be replaced by an integral $\sum_k \rightarrow (L/2 \pi) \int dk$ and converted into an integral over energy $ \int dk = \int (dk/d \epsilon_k) d\epsilon_k$. In the final expression for the current, the two derivatives cancel each other and one has $I_{\Delta \epsilon}= (e/h) \Delta \epsilon$ where $\Delta \epsilon$ is the energy interval corresponding to $\Delta k$. This result states that independently of the form of the 1D band, all energy intervals with the same width within the bandwidth contribute equally to the current.

In the case of the 1D tight-binding chain, the velocity of the electrons goes to zero as the energy approaches the top or the bottom of the band and therefore the contribution of an individual state to the current goes also to zero. This is however compensated by the fact that the density of states is inversely proportional to the velocity and therefore diverges as the energy approaches the top or the bottom of the band, compensating the smaller individual contribution of each state. The same reasoning is followed for negative velocity states which generate a current in the opposite direction. A finite bias implies that the chemical potential for electrons with positive or negative velocities is different (they originate from opposite ends of the system), $\mu_1$ and $\mu_2$ respectively, and the zero temperature net current is given by $I= (e/h) (\mu_1- \mu_2)$. The respective conductance is $G=I/V=I/[(\mu_1- \mu_2)/e]=e^2/h$. At finite temperature the bands are populated according to the Fermi-Dirac distribution $f(\epsilon,\mu)=[\exp[(\epsilon-\mu)/k_BT]+1]^{-1}=f_0(\epsilon - \mu)$ and the current becomes $I= (e/h) \int_{-\infty}^\infty [f_0(\epsilon-\mu_1)- f_0(\epsilon-\mu_2))$. The final ingredient is the introduction of an obstacle (a structural or potential barrier) in the path of the 1D electrons. An electron with energy $\epsilon$ is transmitted through the barrier with probability $|t(\epsilon)|^2 $ as explained above and the current becomes $I= (e/h) \int_{-\infty}^\infty |t(\epsilon)|^2 [f_0(\epsilon-\mu_1)- f_0(\epsilon-\mu_2))$. Since $\mu_1 -\mu_2=eV$, the differential conductance $G=dI/dV$ for spinless fermions on the lattice is given by \begin{equation} \label{condu3} G(T)=\displaystyle\frac{e^2}{h}\int\limits_{-2}^{2} \left(-\frac{df}{d\epsilon}\right)|t(\epsilon)|^2 d\epsilon , \end{equation} where $f=f(\epsilon,\mu)$ is the Fermi-Dirac distribution \cite{Landauer1970}. For zero temperature, $ G(0)=\frac{e^2}{h} |t(\mu)|^2. $

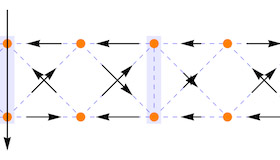
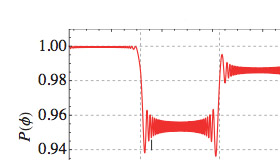
Current configuration in a rhombi chain with two-band spinal elements

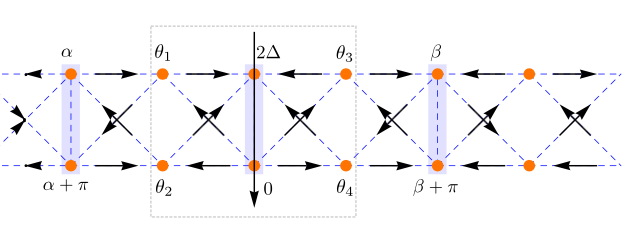
Frustrated Josephson junction (JJ) arrays studies have been to a large extent motivated by the close analogy with frustrated classical spin systems and more recently by the possible relevance of these systems to quantum computation. This analogy requires the conditions of low temperature and symmetric JJs, both in experimental and theoretical studies. Such conditions imply that the superconducting phases are the only variables required to describe the superconducting system. If the Josephson current is studied as a function of temperature, the variation of the magnitudes of the superconducting order parameters has to be taken into account, particularly when asymmetric junctions are present or if, as in the case of the present paper, two-band superconducting elements are introduced in the JJ array. In the case of a JJ array with two-band superconducting elements, besides the usual Josephson tunnelings, one must consider the interband tunnelings, which effectively modify the geometry of the JJ array. In fact, a multiband superconductor can be regarded as a simple realization of a short JJ array. The interband pairings are equivalent to Josephson tunnelings and, for example, a three-band superconductor is analogous to a triangular circuit of asymmetric JJs. Frustration in this case occurs if one or several interband interactions are repulsive since a repulsive interband interaction in a multiband superconductor plays a similar role to that of a π junction in a Josephson junction array.

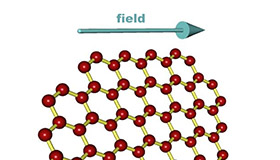
SSH model

The SSH model is the model of choice to illustrate topological transitions in one dimensional models. More complex 1D models are usually analyzed in light of the expected SSH model behavior. The SSH model consists of a 1D tight-binding model with alternating hopping constants $t_{1}$and $t_{2}$, \begin{equation} H=-\sum_{j}\left[t_{1}c_{jA}^{\dagger}c_{jB}+t_{2}c_{jB}^{\dagger}c_{j+1A}+H.c.\right]. \end{equation} where an infinite chain or periodic boundary conditions are assumed. Fourier transforming from the Wannier basis to the basis $\{\vert k;A\rangle,\vert k;B\rangle\}$, the matrix representation of the Hamiltonian becomes \begin{eqnarray*} H(k) & = & \begin{bmatrix}0 & t_{1}+t_{2}e^{-iak}\\ t_{1}+t_{2}e^{iak} & 0 \end{bmatrix}\\ & = & \begin{bmatrix}0 & t_{1}\\ t_{1} & 0 \end{bmatrix}+\begin{bmatrix}0 & t_{2}e^{-iak}\\ t_{2}e^{iak} & 0 \end{bmatrix}\\ & = & \begin{bmatrix}0 & \rho^{*}(k)\\ \rho(k) & 0 \end{bmatrix} \end{eqnarray*} with $\rho(k)=t_{1}+t_{2}e^{iak}=\vert\rho(k)\vert e^{i\phi(k)}$.

Hubbard model

One dimensional models with a Bethe-Ansatz solution fall into the Luttinger liquid universality class. Among these, the most famous example is possibly the Hubbard model. The Hubbard Hamiltonian for a ring with $L$ sites is \begin{equation} H_U = -t \sum_{i,s} (c_{i,s}^\dagger c_{i+1,s} + c_{i+1,s}^\dagger c_{i,s}) + U \sum_i n_{i,\uparrow} n_{i,\downarrow}, \end{equation} where $c_{i,s}^\dagger$ is the fermion creation operator on site $i$ with spin $s$, $n_{i,s}=c_{i,s}^\dagger c_{i,s}$ and $U$ is the repulsive onsite Coulomb interaction. This model is spin rotation invariant. While for general $U/t$, one has to deal with the complicated Bethe-Ansatz solution, it is possible to take a simpler approach in the limits $U \ll t$ and $U \rightarrow \infty$

Localized states in the Mielke lattice

Some other text...

Localized states in the Mielke lattice

Some other text...