Publications
Flux-mediated effective Su-Schrieffer-Heeger model in an impurity decorated diamond chain
In flat-band systems with non-orthogonal compact localized states (CLSs), onsite perturbations couple neighboring CLSs and generate exponentially-decaying impurity states, whose degree of localization depends on lattice parameters. In this work, a diamond chain with constant magnetic flux ...
More
Impurity flat band states in the diamond chain
Flat band (FB) systems, i.e., models hosting dispersionless bands in their energy spectrum, have attracted great interest recently. The eigenstates of these FBs can be written as compact localized states (CLSs), meaning states having finite support only over a small, non-extensive portion of the lattice. When adjacent CLSs of a FB have spatial overlap, ...
More
Exotic edge states of C3 high-fold fermions in honeycomb lattices
A generalization of the graphene honeycomb model to the case where each site in the honeycomb lattice contains a fold degenerate set of eigenstates of the symmetry has been recently proposed to describe several systems, including triangulene crystals and photonic lattices. ...
More
Topological wave equation eigenmodes in continuous 2D periodic geometries
In this paper, we address the topological characterization of the wave equation solutions in continuous two-dimensional (2D) periodic geometries with Neumann or Dirichlet boundary conditions. This characterization is relevant in the context of 2D vibrating membranes and our approach ...
More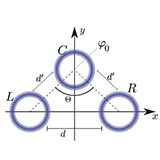
Ultracold atoms carrying orbital angular momentum: Engineering topological phases in lattices
Ultracold atoms carrying Orbital Angular Momentum (OAM) loaded in lattices constitute a promising platform for engineering topological systems either at the single-particle limit or in the presence of interactions. In this review, we report recent progress on this topic with the focus on ...
More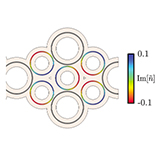
Topological n-root Su–Schrieffer–Heeger model in a non-Hermitian photonic ring system
Square-root topology is one of the newest additions to the ever expanding field of topological insulators (TIs). It characterizes systems that relate to their parent TI through the squaring of their Hamiltonians. Extensions to 2 n -root topology, where n is the number of squaring ...
More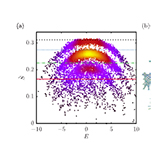
Flat band induced local Hilbert space fragmentation
We demonstrate that a complete class of flat-band lattices with underlying commutative local symmetries exhibit a locally fragmented Hilbert space. The equitable partition theorem ensures distinct parities for the compact localized states (CLSs) present in this class of flat-band lattices a ...
More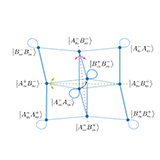
Bosonic orbital Su-Schrieffer-Heeger model in a lattice of rings
We study the topological properties of interacting and noninteracting bosons loaded in the orbital angular momentum states l= 1 in a lattice of rings with alternating distances. At the single-particle level, the two circulation states within each site lead to two decoupled Su-Schrieffer-Heeger lattices with correlated topological phases. ...
More
Kaleidoscopes of Hofstadter Butterflies and Aharonov-Bohm caging from $2^n$-root topology in decorated square lattices
Square-root topology describes models whose topological properties can be revealed upon squaring the Hamiltonian, which produces their respective parent topological insulators. This concept has recently been generalized to $2^n$-root topology, characterizing models where $n$ squaring operations ...
More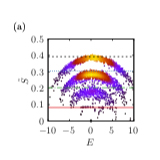
Local Hilbert space fragmentation and weak thermalization in Bose-Hubbard diamond necklaces
Hermitian bipartite models are characterized by the presence of chiral symmetry and by the Lieb's theorem, which derives the number of zero-energy flat bands of the model from the imbalance of sites between its two sublattices. Here, we introduce a class of non-Hermitian models with an arbitrary number of sublattices connected in a non-reciprocal ...
More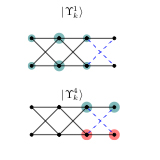
Many-body Aharonov-Bohm caging in a lattice of rings
We study a system of a few ultracold bosons loaded into the states with orbital angular momentum of a one-dimensional staggered lattice of rings. Local eigenstates with winding numbers and form a Creutz ladder with a real dimension and a synthetic one. States with opposite winding numbers in adjacent rings are coupled through complex tunnelings, which can be tuned by modifying the central angle ...
More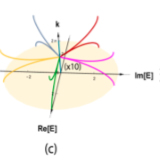
Generalized Lieb's theorem for non-Hermitian n-partite lattices
Hermitian bipartite models are characterized by the presence of chiral symmetry and by the Lieb's theorem, which derives the number of zero-energy flat bands of the model from the imbalance of sites between its two sublattices. Here, we introduce a class of non-Hermitian models with an arbitrary number of sublattices connected in a non-reciprocal ...
More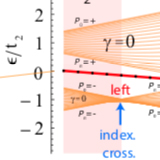
Long-range hopping and indexing assumption in one-dimensional topological insulators
In this paper, we show that the introduction of long-range hoppings in one-dimensional topological insulator models implies that different possibilities of site indexing must be considered when determining the bulk topological invariants in order to avoid the existence of hidden symmetries. ...
More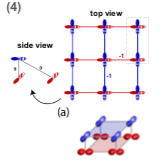
Superconductivity in twisted bilayer quasi-one-dimensional systems with flat bands
Unconventional superconductivity recently observed in twisted bilayer graphene is associated with the presence of van-Hove singularities very close to the Fermi level reflecting the flattening of bands for a set of magic twist angles. In this paper, we address a stack of two identical quasi-one-dimensional layers, each one composed of a set of chains with p-wave orbitals at each site. ...
More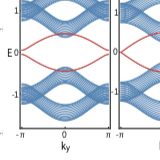
2^n-root weak, Chern and higher-order topological insulators and 2^n-root topological semimetals
Recently, we have introduced in [Phys. Rev. B 103, 235425 (2021)] the concept of 2n-root topology and applied it to one-dimensional (1D) systems. These models require n squaring operations to their Hamiltonians, intercalated with different constant energy downshifts at each level, in order to arrive at a decoupled block corresponding to a known topological insulator (TI) that acts as ...
More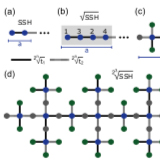
One-dimensional 2^n-root topological insulators and superconductors
Square-root topology is a recently emerged sub-field describing a class of insulators and superconductors whose topological nature is only revealed upon squaring their Hamiltonians, ie, the finite energy edge states of the starting square-root model inherit their topological features from the zero-energy edge states of a known topological insulator/superconductor present in the squared...
More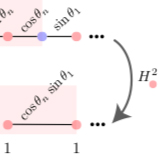
Matryoshka approach to Sine-Cosine topological models
We address a particular set of SSH () models ( being the number of sites in the unit cell) that we designate by Sine-Cosine models [SC ], with hopping terms defined as a sequence of sine-cosine pairs of the form , . These models, when squared, generate a block-diagonal matrix representation with one of the blocks corresponding to a chain with uniform local potentials. ...
More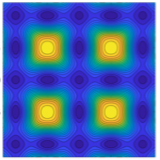
Hubbard models and state preparation in an optical Lieb lattice
Inspired by the growing interest in probing many-body phases in novel two-dimensional lattice geometries we investigate the properties of cold atoms as they could be observed in an optical Lieb lattice. We begin by computing Wannier functions localised at individual sites for a realistic experimental setup, and determining coefficients for a Hubbard-like model. ...
More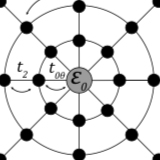
Topologically protected states in a spider web lattice
Topological phases and edge-state topological protection are explicitly related by the bulk-edge correspondence which assumes the existence a real space boundary in one-dimensional (1D), 2D, or 3D systems. Extensions of this picture to systems where the boundary is present in the domain of generalized coordinates may generate unusual topological behavior in real space. In this paper, ...
More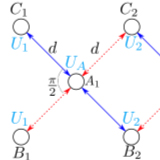
Interaction-induced topological properties of two bosons in flat-band systems
In flat-band systems, destructive interference leads to the localization of noninteracting particles and forbids their motion through the lattice. However, in the presence of interactions the overlap between neighboring single-particle localized eigenstates may enable the propagation of bound pairs of particles. In this work, we show how these interaction-induced hoppings ...
More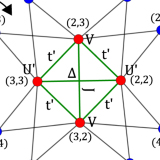
Methods for the construction of interacting many-body Hamiltonians with compact localized states in geometrically frustrated clusters
Adding interactions to many-body Hamiltonians of geometrically frustrated lattices often leads to diminished subspaces of localized states. In this paper, we show how to construct interacting many-body Hamiltonians, starting from the non-interacting tight-binding Hamiltonians, that preserve or even expand these subspaces. The methods ...
More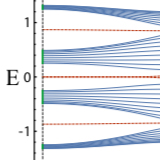
Analytical solution of open crystalline linear 1D tight-binding models
A method for finding the exact analytical solutions for the bulk and edge energy levels and corresponding eigenstates for all commensurate Aubry–André/Harper single-particle models under open boundary conditions is presented here, both for integer and non-integer number of unit cells. ...
More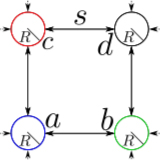
Second-order topological corner states with ultracold atoms carrying orbital angular momentum in optical lattices
We propose a realization of a two-dimensional higher-order topological insulator with ultracold atoms loaded into orbital angular momentum (OAM) states of an optical lattice. The symmetries of the OAM states induce relative phases in the tunneling amplitudes that allow to describe the system in terms of two decoupled lattice models. ...
More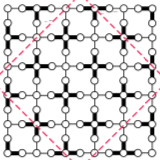
Enhanced localization and protection of topological edge states due to geometric frustration
Topologically nontrivial phases are linked to the appearance of localized modes in the boundaries of an open insulator. On the other hand, the existence of geometric frustration gives rise to degenerate localized bulk states. The interplay of these two phenomena may, in principle, result in an enhanced protection/localization of edge states. In this paper, we study a two-dimensional Lieb-based ...
More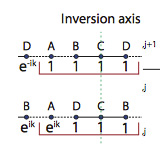
One-dimensional topological insulators with noncentered inversion symmetry axis
In this paper, we discuss the characteristic features of 1D topological insulators with inversion symmetry but non-centered inversion axis in the unit cell, for any choice of the unit cell. In these systems, the global inversion operation generates a $k$-dependent inversion operator within the unit cell and this implies a non-quantized Zak's phase both for the trivial ...
More
Hole-localized states in interacting geometrically frustrated systems
Many-body localized states are shown to exist in geometrically frustrated lattices if the interacting Hamiltonian generates a network of transition matrix elements between many-body Wannier states with bubblelike structures. We show that such structures occur in the U/t=∞ Hubbard model on the Lieb and kagome lattices and ...
More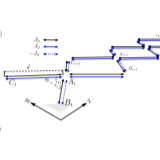
Topological edge states and Aharanov-Bohm caging with ultracold atoms carrying orbital angular momentum
We show that bosonic atoms loaded into orbital angular momentum l= 1 states of a lattice in a diamond-chain geometry provide a flexible and simple platform for exploring a range of topological effects. This system exhibits robust edge states that persist across the gap-closing points, indicating the absence of a topological transition. ...
More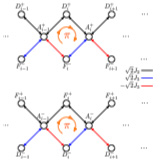
Topological edge states with ultracold atoms carrying orbital angular momentum in a diamond chain
We study the single-particle properties of a system formed by ultracold atoms loaded into the manifold of l= 1 orbital angular momentum (OAM) states of an optical lattice with a diamond-chain geometry. Through a series of successive basis rotations, we show that the OAM degree of freedom ...
More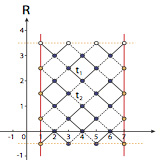
Topological bound states in interacting Su-Schrieffer-Heeger rings
We study two-particle states in a Su-Shrieffer-Heeger (SSH) chain with periodic boundary conditions and nearest-neighbor (NN) interactions. The system is mapped into a problem of a single particle in a two-dimensional (2D) SSH lattice with potential walls along specific edges. The 2D SSH model has a trivial Chern number but a non-trivial Zak's phase, the one-dimensional (1D) topological invariant, along ...
More
Generalization of Zak's phase for lattice models with non-centered inversion symmetry axis
We show how the presence of inversion symmetry in a one-dimensional (1D) lattice model is not a sufficient condition for a quantized Zak's phase. This is only the case when the inversion axis is at the center of the unit cell. When the inversion axis is not at the center, the modified inversion operator ...
More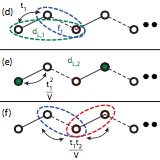
Multi-hole edge states in SSH chains with interactions
We address the effect of nearest-neighbor (NN) interactions on the topological properties of the Su-Schrieffer-Heeger (SSH) chain, with alternating hopping amplitudes t1 and t2. Both numerically and analytically, we show that the presence of interactions induces phase transitions between topologically different regimes. In the particular case of one-hole excitations in a half-filled SSH chain, ...
More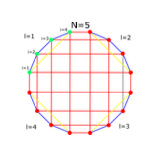
Notes on the Kitaev -> Tight-binding correspondence
In this project, we study the properties of a non-trivial topological system which exhibits localized edge states. In our study, we adress the Kitaev chain, a one-dimensional chain of atoms deposited on top of a p-wave superconductor that induces superconductivity in the chain by proximity effect. We establish a correspondence between the Kitaev chain and a tight-binding lattice with a particular geometry for a particular case of the system parameters. This correspondence allows one....
More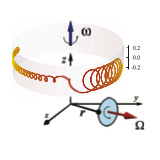
Evolution of localized states in Lieb lattices under time-dependent magnetic fields
We study the slow time evolution of localized states of the open-boundary Lieb lattice when a magnetic flux is applied perpendicularly to the lattice and increased linearly in time. In this system, Dirac cones periodically disappear, reappear, and touch the flat band as the flux increases. We show that the slow time evolution of a localized state in this system is analogous to that of a zero-energy state ...
More
Edge currents in frustrated Josephson junction ladders
We present a numerical study of quasi-1D frustrated Josephson junction ladders with diagonal couplings and open boundary conditions, in the large capacitance limit. We derive a correspondence between the energy of this Josephson junction ladder and the expectation value of the Hamiltonian of an analogous tight-binding model, and show how the overall superconducting state of the chain is equivalent ...
More
Perversions with a twist
Perversions connecting two helices with symmetric handedness are a common occurrence in nature, for example in tendrils. These defects can be found in our day life decorating ribbon gifts or when plants use tendrils to attach to a support. Perversions arise when clamped elastic filaments coil into a helical shape but have to conserve zero overall twist. We investigate whether other types ...
More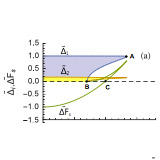
Pauli limiting and metastability regions of superconducting graphene and intercalated graphite superconductors
We present a study of metastability regions in the in-plane magnetic field \textit{versus} temperature phase diagram of graphene and intercalated graphite superconductors. Due to the vanishing density of states, undoped graphene requires a finite BCS interaction $V_{c}$ to become superconducting ...
More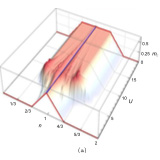
Spin and charge density waves in the Lieb lattice
We study the mean-field phase diagram of the two-dimensional (2D) Hubbard model in the Lieb lattice allowing for spin and charge density waves. Previous studies of this diagram have shown that the mean-field magnetization surprisingly deviates from the value predicted by Lieb's theorem as the on-site repulsive Coulomb interaction ($U$) becomes smaller ...
More
Origami rules for the construction of localized eigenstates of the Hubbard model in decorated lattices
We present a method of construction of exact localized many-body eigenstates of the Hubbard model in decorated lattices, both for $U=0$ and $U\rightarrow\infty$. These states are localized in what concerns both hole and particle movement. The starting point of the method is the construction of a plaquette or a set of plaquettes with a higher symmetry than that of the whole lattice....
More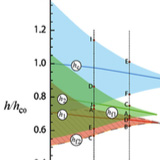
In-plane magnetic field vs. temperature phase diagram of a quasi-2D frustrated multiband superconductor
Motivated by the recent discovery of iron-based superconductors, with high critical temperatures and multiple bands crossing the Fermi level, we address the conditions for the presence of chiral superconducting phases configurations in the in-plane magnetic field vs. temperature phase diagram of a quasi-2D frustrated three-band superconductor...
More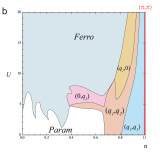
Magnetic phase diagram of the Hubbard model in the Lieb lattice
We study the mean-field phase diagram of the repulsive Hubbard model in the Lieb lattice. Far from half-filling, the most stable phases are paramagnetism for low on-site interaction U/t and ferromagnetism for high U/t, as in the case of the mean-field phase diagram of the square lattice Hubbard model obtained by Dzierzawa (1991) ...
More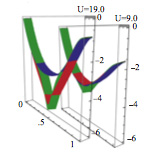
Spiral ferrimagnetic phases in the two-dimensional Hubbard model
We address the possibility of spiral ferrimagnetic phases in the mean-field phase diagram of the two-dimensional (2D) Hubbard model. For intermediate values of the interaction U (6≲U/t≲116≲U/t≲11) and doping n, a spiral ferrimagnetic phase is the most stable phase in the (n,U) phase diagram. Higher values of U lead to a non-spiral ferrimagnetic phase. ...
More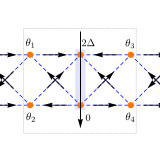
Chiral classical states in a rhombus and a rhombi chain of Josephson junctions with two- band superconducting elements
We present a study of Josephson junctions arrays with two-band superconducting elements in the high- capacitance limit. We consider two particular geometries for these arrays: a single rhombus and a rhombi chain with two-band superconducting elements at the spinal positions. We show that the rhombus shaped JJ circuit and the rhombi chain can...
More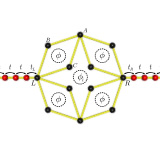
Conductance through geometrically frustrated itinerant electronic systems
We study a two terminal electronic conductance through an AB2 ring which is an example of the family of itinerant geometrically frustrated electronic systems. These systems are characterized by the existence of localized states with nodes in the probability density. We show that such states lead to distinct features in the conductance. ...
More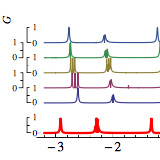
Simple approach for the two-terminal conductance through interacting clusters
We present a new method for the determination of the two-terminal differential conductance through an interacting cluster, where one maps the interacting cluster into a non-interacting cluster of M independent sites (where M is the number of cluster states with one particle more or less than the ground state of the cluster), with different onsite energy and connected to the leads with ...
More