Computing polynomials in C code

• Intro
• The NIST Tables
• Polynomial computation
• Code implementation
• Results
• Conclusion
• Resources

Intro

Computing numerical values using polynomials is common in many instrumentation applications. Polynomial expressions allow to create a numerical approximation to the relationship between two physical variables, even when this relationship is complex.

The NIST Tables

For the case of thermocouples, the relation between the temperature detected by the thermocouple and the generated emf (electromotive force) is described by a polynomial expression. The NIST ITS-90 Thermocouple Database page provides access to the reference functions and tables of thermocouple emf versus temperature that have been adopted as standards by the American Society for Testing and Materials (ASTM) and the International Electrotechnical Commission (IEC). These reference functions establish the relationship between temperature (in degrees Celsius) and voltage (in mV) for the several types of thermocouples in both direct and inverse way, as a polynomial relationship.

The direct functions give the thermoelectric voltage $E$ as a function of the temperature $t_{90}$

$$E = \sum_{i=0}^{n} c_i (t_{90})^i$$

and the inverse functions, the temperature as a function of the thermoelectric voltage:

$$t_{90} = d_0 + d_1 E + d_2 E^2 + \ldots + d_n E^n$$

In the equations above, $t_{90}$ refers to the temperature in °C in the International Temperature Scale of 1990 (ITS-90), defined by the BIPM.

Depending on the type of thermocouple, the polynomial degree can be as high as 14, as in the case of the T type thermocouple.

Polynomial computation

When implementing the NIST reference functions in code (or any other polynomial expression), the most straightforward solution would be to write the polynomial in the canonical form (for simplicity, a fourth order polynomial is shown):

$$t_{90} = d_0 + d_1 \cdot E + d_2 \cdot E^2 + d_3 \cdot E^3 + d_4 \cdot E^4$$

The equation above contains a total of 10 multiplications and 4 sums. For the general case, a polynomial of order $n$ will require a total of $(n^2+n)/2$ multiplications and $n$ sums.

The coefficient values, due to their nature, are required to be floating point values. Multiplying floating point type data is usually an expensive operation in terms of micro-controller clock cycles, particularly when a Floating Point Unit is not available, which is the case of most micro-controllers. As such, an implementation with fewer products would be preferable. That is possible by factorizing the polynomial, leading to:

$$t_{90} = d_0 + E (d_1 + E(d_2 + E(d_3 + d_4 E)))$$

The number of multiplications is now reduced to 4 and the number of sums is 4. For the general case of an $n$ order polynomial, the number of products is $n$, as well as the number of sums. The number of required multiplications was reduced from an order of $n^2$ to an order of $n$.

Code implementation

The module nist_poly implements NIST inverse functions for the type J thermocouple, using two functions, one with the implementation using the canonical form and another with the factorized form. In both implementations, the array NIST_J_d[] contains the $d$ coefficients for the inverse polynomial of the J type thermocouple.

/* Array with NIST coefficients */
/* See: https://srdata.nist.gov/its90/main/ */
double  NIST_J_d[] = {
  0.000000E+00,
  1.978425E+01,
  -2.001204E-01,
  1.036969E-02,
  -2.549687E-04,
  3.585153E-06,
  -5.344285E-08,
  5.099890E-10,
  0.000000E+00
};

In NIST_J_inv_poly(), the function is implemented in the canonical form:

/*
 * Computes temperature by a polynomial
 */
double NIST_J_inv_poly(double voltage)
{
  double Theta=0;
  size_t i;

  for (i = 0; i < count; i++) {
    Theta +=  NIST_J_d[i]*pow(voltage,i);
  }

  return Theta;

}

NIST_J_inv_fact implements the same function but in the factorized form:

/*
 * Computes temperature by a product factorization.
 */
double NIST_J_inv_fact(double voltage)
{
  double Theta=0;
  double temp = 0;
  int i;

  for (i = 8; i >= 0; i--) {
    temp = NIST_J_d[i] +voltage*temp;
  }

  Theta = temp;

  return Theta;

}

Results

The difference in computation time can measured by the following code, that causes one micro-controller output pin to be ON for the time each function takes to execute.

while (1) {
    /* Test execution time for polynomial version */
    LATCbits.LATC2 = 1;
    Theta_poly = NIST_J_inv_poly(voltage);
    LATCbits.LATC2 = 0;

    /* Test execution time for factorized version */
    LATCbits.LATC3 = 1;
    Theta_fact = NIST_J_inv_fact(voltage);
    LATCbits.LATC3 = 0;

}

The results are shown in the following figure. Data was collected in a system with a Microchip’s PIC32MX795F512L, running with a 80 MHz system clock. Channel A is connected to LATC2 pin and Channel B to LATC3 pin:

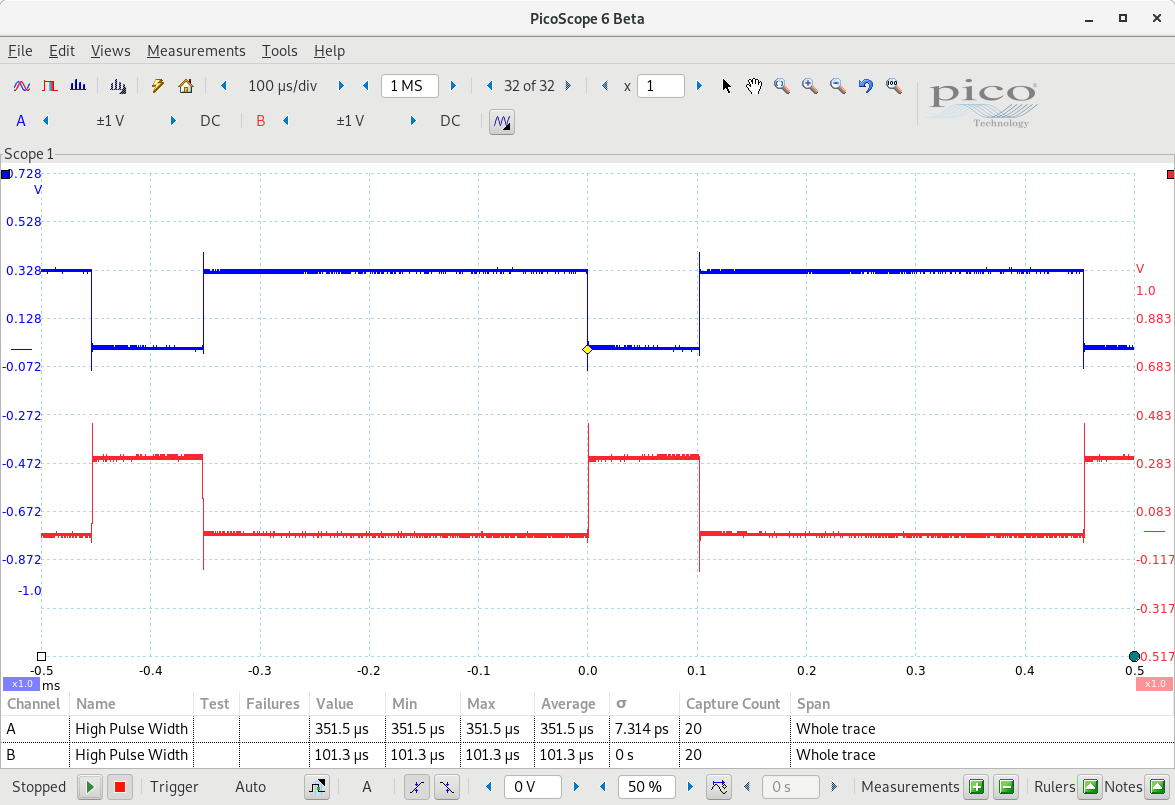
The polynomial version takes approximately 350 µs and the factorized version about 100 µs, an improvement of 3.5 times the execution time.

Conclusion

The factorized implementation of the NIST polynomial allowed an improvement of 3.5 times in the execution time of the reference function. This improvement is achieved by avoiding unnecessary computations, in this case, by reducing the number of products, an operation that is usually costly in terms of CPU time in micro-controllers.

Resources

• nist_poly.c: source file with the function code.
• nist_poly.h: header file.
• NIST_tables.X: MPLab X project files.