Tables of values of pi(x) and of pi2(x)
Introduction
Some of my computational projects require the evaluation of a function for each prime number inside a given interval. To guard against random computational errors (usually originated in the memory subsystem), the computations inside each interval should be done at least twice and should be discarded if the results disagree. A much less reliable and less expensive alternative is to verify if the number of primes inside the interval being analyzed agrees with an independent count obtained by other means. This number of primes can be computed easily if a table of values of the prime counting function pi(x), which counts the number of primes not larger than x, contains entries for the two endpoints of the interval.
When p and p+2 are both prime, they are said to form a twin prime pair. In contrast to pi(x), the only know way to count the number of twin prime pairs with p<=x, denoted by pi2(x), is to generate them all.
Because freely available extensive tables of values of pi(x) and of pi2(x) are quite rare (besides my own tables, Thomas R. Nicely's tables are the only extensive ones I know of), in order to be able to check my computations I made the tables described below. For pi(x), these tables were made in part with my inefficient implementation of the Lagarias-Miller-Odlyzko variant of the Meissel-Lehmer method, described in [1], and in part with my efficient implementation of the Deléglise-Rivat variant of the same method, described in [2] and in [3]. For pi2(x), the tables are a by-product of my Goldbach conjecture verification project.
Tables of values of pi(x)
(6330224 entries in the database; some entries computed by Thomas Nicely.)
- The first 76 values of pi(2^k) [2k, compressed with gzip]
» Last update made on November 20, 2012
» Partially double-checked by the pi(x) program - The first 23 values of pi(10^k) [1k, compressed with gzip]
» Last update made on March 28, 2007
» Partially double-checked by the pi(x) program and by Xavier Gourdon's computations - The first 10000 values of pi(k·10) [83k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^2) [99k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^3) [109k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^4) [118k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^5) [127k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^6) [135k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^7) [142k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^8) [148k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^9) [156k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by a segmented sieve of Eratosthenes - The first 10000 values of pi(k·10^10) [163k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by the least primitive roots project - The first 10000 values of pi(k·10^11) [172k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by the pi(x) program - The first 10000 values of pi(k·10^12) [179k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by the Goldbach conjecture verification project - The first 10000 values of pi(k·10^13) [188k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by the Goldbach conjecture verification project - The first 10000 values of pi(k·10^14) [197k, compressed with gzip]
» Last update made on January 23, 2005
» Double-checked by the pi(x) program, double-checked by the Goldbach conjecture verification project - The first 10000 values of pi(k·10^15) [205k, compressed with gzip]
» Last update made on January 23, 2005
» Partially double-checked by the pi(x) program - The first 10000 values of pi(k·10^16) [212k, compressed with gzip]
» Last update made on December 10, 2010
» Partially double-checked by the pi(x) program - The first 1000 values of pi(k·10^17) [23k, compressed with gzip]
» Last update made on March 1, 2006
» Partially double-checked by the pi(x) program - The first 100 values of pi(k·10^18) [3k, compressed with gzip]
» Last update made on September 29, 2005
» Partially double-checked by the pi(x) program - The first 100 values of pi(k·10^19) [3k, compressed with gzip]
» Last update made on May 12, 2006 - The first 100 values of pi(k·10^20) [3k, compressed with gzip]
» Last update made on December 22, 2010 - The first 100 values of pi(k·10^21) [3k, compressed with gzip]
» Last update made on May 18, 2012 - The first 10 values of pi(k·10^22) [1k, compressed with gzip]
» Last update made on December 7, 2008
Warning: Some of the values of pi(x) were double-checked by running the same program twice, usually in the same machine, using the same internal parameters. Thus, they have been double-checked against random machine errors, but not against algorithmic or consistent machine errors (such as the infamous Pentium fdiv hardware bug). Nonetheless, I am 99.99% confident that all results presented in these tables are correct. All cross-checks (different machines and/or different internal parameters) performed so far produced exactly the same results.
Comparison between pi(x) and li(x)
The prime number theorem states that pi(x) does not deviate much from the so-called logarithmic integral li(x), defined by
x dt
li(x) = P.V. INTEGRAL ------ .
0 log(t)
It is known that li(x)-pi(x) changes sign infinitely often. However, it is also known that negative values of li(x)-pi(x) are extremelly rare [4]. Let
li(x) - pi(x)
H(x) = 2 ------------- .
li(sqrt(x))
We took the liberty of replacing pi(sqrt(x)) by its approximation li(sqrt(x)) in the definition of H(x); this was done only to simplify its computation. It was shown in [5] than H(x) can be approximated quite well by
sin(t log(x))
H(x,L) = 1 + 2 SUM ------------- ,
0 < t < L t
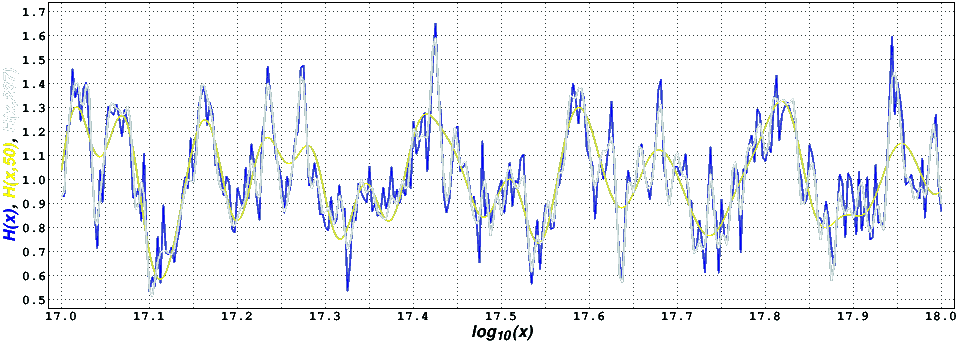
where the sum is over the imaginary part of the roots on the upper half, up to height L, of the critical line of the zeta function. There exists a more precise formula, in which the zeros are only required to be on the critical strip. The first 10^13 zeros are known to lie on the critical line, as shown in 2004 by Xavier Gourdon. The following figure presents the function H(x) computed using the data in our pi(x) tables (blue curve), as well as its approximation using only the first ten and the first one hundred zeros of the zeta function on the upper part of the critical line (yellow curve and white curve, respectively). It can be seen in the figure that the approximation captures quite well the "low-frequency" behaviour of H(x). When much more zeros are used (not shown), the two curves become almost indistinguishable.
Tables of values of pi2(x)
(6152527 entries in the database; some entries computed by Thomas Nicely.)
- The first 61 values of pi2(2^k) [1k, compressed with gzip]
» Last update made on August 31, 2011 - The first 18 values of pi2(10^k) [1k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10) [63k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^2) [81k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^3) [98k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^4) [108k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^5) [117k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^6) [127k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^7) [132k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^8) [143k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^9) [147k, compressed with gzip]
» Last update made on December 12, 2008 - The first 10000 values of pi2(k·10^10) [155k, compressed with gzip]
» Last update made on December 15, 2008 - The first 10000 values of pi2(k·10^11) [164k, compressed with gzip]
» Last update made on January 19, 2009 - The first 10000 values of pi2(k·10^12) [173k, compressed with gzip]
» Last update made on January 23, 2005
» Computed and double-checked by the Goldbach conjecture verification project - The first 10000 values of pi2(k·10^13) [179k, compressed with gzip]
» Last update made on January 23, 2005
» Computed and double-checked by the Goldbach conjecture verification project - The first 10000 values of pi2(k·10^14) [185k, compressed with gzip]
» Last update made on March 1, 2008
» Computed by the Goldbach conjecture verification project - The first 4000 values of pi2(k·10^15) [78k, compressed with gzip]
» Last update made on April 6, 2012
» Computed by the Goldbach conjecture verification project
Warning: The values of pi2(x) for x>357425·10^12 reported in these tables before March 1, 2008, were too small (by one).
Tables of values of pi(x) mod 2
Using the ideas of [6], it is possible to compute pi(x) mod 2 quickly using a very simple program. Using the ideas of section 2.1 of that paper, possibly coupled with a way to compute quickly several values of the summation of the Möbius function [7], would make the program even quicker. The results presented below were produced by our initial simple implementation, which has a computational complexity of O(x^(0.5+ε)).
- Some values of pi(x) mod 2 [8KiB, compressed with gzip]
» Last update made on August 2, 2013
Estimates of pi(x) for "large" values of x
Using Riemann's exact formula for pi(x) and the first 10^9 zeros of the zeta function on the critical line, accurate to 20 digits after the decimal point, we made a computer program able to estimate the value of pi(x) for x up to about 10^30. Assuming that the values of t log(x) are uniformly distributed modulo 2pi, where t is, as before, the imaginary part of the zero, it is possible to model the terms not used in the formula as a Gaussian random variable with zero mean and an approximate standard deviation which is easy to compute. Unfortunately, this standard deviation decreases slowly with the number of zeros used, to the point that one hundred times the number of zeros gives us less than one extra digit of precision. The estimates in the following table should be compared to the exact values in the tables given above (of course, for the values of x for which exact values are known).
- Estimate of some values of pi(x) [66KiB, compressed with gzip]
» Last update made on December 11, 2012
References
| [1] | J. C. Lagarias, V. S. Miller, and Andrew Odlyzko, Computing pi(x): the Meissel-Lehmer method, Mathematics of Computation, vol. 44, no. 170, pp. 537-560, April 1985. |
| [2] | M. Deléglise and J. Rivat, Computing pi(x): the Meissel, Lehmer, Lagarias, Miller, Odlyzko method, Mathematics of Computation, vol. 65, no. 213, pp. 235-245, January 1996. |
| [3] | Tomás Oliveira e Silva, Computing pi(x): the combinatorial method, Revista do DETUA, vol. 4, no. 6, pp. 759-768, March 2006. |
| [4] | Carter Bays and Richard H. Hudson, A new bound for the smallest x with pi(x)>li(x), Mathematics of Computation, vol. 69, no. 231, pp. 1285-1296, 2000. |
| [5] | Carter Bays and Richard H. Hudson, Zeroes of Dirichlet L-functions and irregularities in the distribution of primes, Mathematics of Computation, vol. 69, no. 230, pp. 861-866, 2000. |
| [6] | Terence Tao, Ernest Croot III, and Harald Helfgott, Deterministic methods to find primes, Mathematics of Computation, published electronically on August 23, 2011. |
| [7] | Mark Deléglise and Joël Rivat, Computing the Summation of the Möbius function, Experimental Mathematics, Vol. 5, No. 4, pp. 291-295, 1996. |
Additional links
- The prime pages.
- Distributed computations of pi(x) for large values of x.
- My Goldbach conjecture verification page.
- My prime gaps page.
- My least primitive roots page.
- My simple but fast implementation of the segmented sieve of Eratosthenes.