Goldbach conjecture verification
Introduction
The Goldbach conjecture is one of the oldest unsolved problems in number theory [1, problem C1]. In its modern form, it states that every even number larger than two can be expressed as a sum of two prime numbers.
Let n be an even number larger than two, and let n=p+q, with p and q prime numbers, p<=q, be a Goldbach partition of n. Let r(n) be the number of Goldbach partitions of n. The number of ways of writing n as a sum of two prime numbers, when the order of the two primes is important, is thus R(n)=2r(n) when n/2 is not a prime and is R(n)=2r(n)-1 when n/2 is a prime. The Goldbach conjecture states that r(n)>0, or, equivalently, that R(n)>0, for every even n larger than two.
In their famous memoir [2, conjecture A], Hardy and Littlewood conjectured that when n tends to infinity, R(n) tends asymptotically to (i.e., the ratio of the two functions tends to one)
n p-1
N2(n) = 2 C ---------------- PRODUCT --- ,
twin (log n)(log n-2) p odd prime p-2
divisor of n
where
p(p-2)
C = PRODUCT ------- = 0.66016181584686957392...
twin p odd prime (p-1)^2
is the twin primes constant. In [3], Crandall and Pomerance suggest replacing the factor
n
----------------
(log n)(log n-2)
appearing in the formula of N2(n) by the asymptotically equivalent factor
n-2 dx
INTEGRAL --------------- .
2 log(x) log(n-x)
The numerical evidence supporting this conjectured asymptotic formula is very strong. Up to 10^10, the Crandall-Pomerance formula does not deviate from R(n) by more than 40150, and up to 2^40 it does not deviate from R(n) by more than 401900.
Let us order the r(n) Goldbach partitions of n by increasing order of the smallest prime of the partition. More precisely, let us denote the two primes of the i-th Goldbach partition of n by p(n;i) and q(n;i), with p(n;i) <= q(n;i) and p(n;i) < p(n;i+1). In order to verify the Goldbach conjecture for a given n, it is sufficient to find one of its Goldbach partitions. Our strategy will be to find the minimal Goldbach partition n=p(n;1)+q(n;1), i.e., the one that uses the smallest possible prime number p(n)=p(n;1). As in [4], for every prime q we will denote by S(q) the least even number n such that p(n)=q.
News
February 1, 2005: 2·10^17 reached.
March 20, 2005: 10^17 double checked.
December 26, 2005: 3·10^17 reached.
June 5, 2006: 4·10^17 reached.
September 28, 2006: interval between 7·10^17 and 10^18 checked.
February 19, 2007: 5·10^17 reached.
February 23, 2007: interval between 6·10^17 and 7·10^17 checked.
April 25, 2007: 10^18 reached.
February 16, 2008: 11·10^17 reached.
July 14, 2008: 12·10^17 reached.
July 24, 2009: 15·10^17 reached.
December 23, 2009: 16·10^17 reached.
January 5, 2010: interval between 19·10^17 and 20·10^17 checked.
March 24, 2010: interval between 18·10^17 and 19·10^17 checked.
August 24, 2010: interval between 17·10^17 and 18·10^17 checked.
November 6, 2010: 2·10^18 reached.
May 24, 2011: 22·10^17 reached.
July 31, 2011: 25·10^17 reached.
September 13, 2011: 26·10^17 reached.
November 30, 2011: discovery of the minimal Goldbach partition 2795935116574469638=9629+P19.
January 16, 2012: discovery of the minimal Goldbach partition 3325581707333960528=9781+P19.
February 6, 2012: 34·10^17 reached.
February 13, 2012: 35·10^17 reached.
April 4, 2012: 4·10^18, our desired verification limit, reached.
June 18, 2012: 2·10^17 double checked.
September 7, 2012: 3·10^17 double checked.
May 26, 2013: 4·10^17 double checked. No more double checking will be done in
the near future.
Computational results
We have implemented a program that finds the minimal Goldbach partition of every even integer larger than four. In order to do this efficiently, the computation intensive parts of the program were written in assembly language (for the IA32 instruction set). A very efficient cache friendly implementation of the segmented sieve of Eratosthenes was used to generate the prime numbers (see our speed comparison chart [23KiB, PDF] between several Intel and AMD CPUs). For each interval of 10^12 integers, we record the number of times each (small) prime is used in a minimal Goldbach partition, as well as the even integer where it was first needed. Because it takes very little extra time, we also record information about the gaps between consecutive primes, viz., how many times each gap occurs, and its first occurrence. On a single core of a 3.3GHz core i3 processor, testing an interval of 10^12 integers near 10^18 takes close to 48 minutes. The execution time of the program grows very slowly, like log(N), where N is the last integer of the interval being tested, and it uses an amount of memory that is roughly given by 13 sqrt(N) / log(N). The program ran on the spare time of many computers, either under GNU/Linux or under Windows XP. We have reached 2·10^18 in November 2010, and in April 2012 have finally reached 4·10^18.
The following table presents an overview of the current status of this massive computation. Each cell represents an interval of 10^15; its background color indicates its computational status (green for double-checked, yellow for single-checked, and red for not yet done or not yet fully checked), and its brightness indicates if counts of the primes in each of the 32 residue classes modulo 120 are available (bright) or not (not so bright) to perform an initial check of the correctness of the computation on each interval of 10^15 (prime counts for each interval of 10^12 are also available to perform correctness checks).
| 0000 | 0001 | 0002 | 0003 | 0004 | 0005 | 0006 | 0007 | 0008 | 0009 | 0010 | 0011 | 0012 | 0013 | 0014 | 0015 | 0016 | 0017 | 0018 | 0019 |
| ... (same state) ... | |||||||||||||||||||
| 0380 | 0381 | 0382 | 0383 | 0384 | 0385 | 0386 | 0387 | 0388 | 0389 | 0390 | 0391 | 0392 | 0393 | 0394 | 0395 | 0396 | 0397 | 0398 | 0399 |
| 0400 | 0401 | 0402 | 0403 | 0404 | 0405 | 0406 | 0407 | 0408 | 0409 | 0410 | 0411 | 0412 | 0413 | 0414 | 0415 | 0416 | 0417 | 0418 | 0419 |
| ... (same state) ... | |||||||||||||||||||
| 0960 | 0961 | 0962 | 0963 | 0964 | 0965 | 0966 | 0967 | 0968 | 0969 | 0970 | 0971 | 0972 | 0973 | 0974 | 0975 | 0976 | 0977 | 0978 | 0979 |
| 0980 | 0981 | 0982 | 0983 | 0984 | 0985 | 0986 | 0987 | 0988 | 0989 | 0990 | 0991 | 0992 | 0993 | 0994 | 0995 | 0996 | 0997 | 0998 | 0999 |
| 1000 | 1001 | 1002 | 1003 | 1004 | 1005 | 1006 | 1007 | 1008 | 1009 | 1010 | 1011 | 1012 | 1013 | 1014 | 1015 | 1016 | 1017 | 1018 | 1019 |
| ... (same state) ... | |||||||||||||||||||
| 1160 | 1161 | 1162 | 1163 | 1164 | 1165 | 1166 | 1167 | 1168 | 1169 | 1170 | 1171 | 1172 | 1173 | 1174 | 1175 | 1176 | 1177 | 1178 | 1179 |
| 1180 | 1181 | 1182 | 1183 | 1184 | 1185 | 1186 | 1187 | 1188 | 1189 | 1190 | 1191 | 1192 | 1193 | 1194 | 1195 | 1196 | 1197 | 1198 | 1199 |
| 1200 | 1201 | 1202 | 1203 | 1204 | 1205 | 1206 | 1207 | 1208 | 1209 | 1210 | 1211 | 1212 | 1213 | 1214 | 1215 | 1216 | 1217 | 1218 | 1219 |
| 1220 | 1221 | 1222 | 1223 | 1224 | 1225 | 1226 | 1227 | 1228 | 1229 | 1230 | 1231 | 1232 | 1233 | 1234 | 1235 | 1236 | 1237 | 1238 | 1239 |
| ... (same state) ... | |||||||||||||||||||
| 1380 | 1381 | 1382 | 1383 | 1384 | 1385 | 1386 | 1387 | 1388 | 1389 | 1390 | 1391 | 1392 | 1393 | 1394 | 1395 | 1396 | 1397 | 1398 | 1399 |
| 1400 | 1401 | 1402 | 1403 | 1404 | 1405 | 1406 | 1407 | 1408 | 1409 | 1410 | 1411 | 1412 | 1413 | 1414 | 1415 | 1416 | 1417 | 1418 | 1419 |
| 1420 | 1421 | 1422 | 1423 | 1424 | 1425 | 1426 | 1427 | 1428 | 1429 | 1430 | 1431 | 1432 | 1433 | 1434 | 1435 | 1436 | 1437 | 1438 | 1439 |
| 1440 | 1441 | 1442 | 1443 | 1444 | 1445 | 1446 | 1447 | 1448 | 1449 | 1450 | 1451 | 1452 | 1453 | 1454 | 1455 | 1456 | 1457 | 1458 | 1459 |
| 1460 | 1461 | 1462 | 1463 | 1464 | 1465 | 1466 | 1467 | 1468 | 1469 | 1470 | 1471 | 1472 | 1473 | 1474 | 1475 | 1476 | 1477 | 1478 | 1479 |
| 1480 | 1481 | 1482 | 1483 | 1484 | 1485 | 1486 | 1487 | 1488 | 1489 | 1490 | 1491 | 1492 | 1493 | 1494 | 1495 | 1496 | 1497 | 1498 | 1499 |
| 1500 | 1501 | 1502 | 1503 | 1504 | 1505 | 1506 | 1507 | 1508 | 1509 | 1510 | 1511 | 1512 | 1513 | 1514 | 1515 | 1516 | 1517 | 1518 | 1519 |
| ... (same state) ... | |||||||||||||||||||
| 1580 | 1581 | 1582 | 1583 | 1584 | 1585 | 1586 | 1587 | 1588 | 1589 | 1590 | 1591 | 1592 | 1593 | 1594 | 1595 | 1596 | 1597 | 1598 | 1599 |
| 1600 | 1601 | 1602 | 1603 | 1604 | 1605 | 1606 | 1607 | 1608 | 1609 | 1610 | 1611 | 1612 | 1613 | 1614 | 1615 | 1616 | 1617 | 1618 | 1619 |
| 1620 | 1621 | 1622 | 1623 | 1624 | 1625 | 1626 | 1627 | 1628 | 1629 | 1630 | 1631 | 1632 | 1633 | 1634 | 1635 | 1636 | 1637 | 1638 | 1639 |
| ... (same state) ... | |||||||||||||||||||
| 1720 | 1721 | 1722 | 1723 | 1724 | 1725 | 1726 | 1727 | 1728 | 1729 | 1730 | 1731 | 1732 | 1733 | 1734 | 1735 | 1736 | 1737 | 1738 | 1739 |
| 1740 | 1741 | 1742 | 1743 | 1744 | 1745 | 1746 | 1747 | 1748 | 1749 | 1750 | 1751 | 1752 | 1753 | 1754 | 1755 | 1756 | 1757 | 1758 | 1759 |
| 1760 | 1761 | 1762 | 1763 | 1764 | 1765 | 1766 | 1767 | 1768 | 1769 | 1770 | 1771 | 1772 | 1773 | 1774 | 1775 | 1776 | 1777 | 1778 | 1779 |
| 1780 | 1781 | 1782 | 1783 | 1784 | 1785 | 1786 | 1787 | 1788 | 1789 | 1790 | 1791 | 1792 | 1793 | 1794 | 1795 | 1796 | 1797 | 1798 | 1799 |
| 1800 | 1801 | 1802 | 1803 | 1804 | 1805 | 1806 | 1807 | 1808 | 1809 | 1810 | 1811 | 1812 | 1813 | 1814 | 1815 | 1816 | 1817 | 1818 | 1819 |
| ... (same state) ... | |||||||||||||||||||
| 1900 | 1901 | 1902 | 1903 | 1904 | 1905 | 1906 | 1907 | 1908 | 1909 | 1910 | 1911 | 1912 | 1913 | 1914 | 1915 | 1916 | 1917 | 1918 | 1919 |
| 1920 | 1921 | 1922 | 1923 | 1924 | 1925 | 1926 | 1927 | 1928 | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 | 1938 | 1939 |
| 1940 | 1941 | 1942 | 1943 | 1944 | 1945 | 1946 | 1947 | 1948 | 1949 | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 | 1959 |
| 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 | 1970 | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 |
| 1980 | 1981 | 1982 | 1983 | 1984 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| ... (same state) ... | |||||||||||||||||||
| 2220 | 2221 | 2222 | 2223 | 2224 | 2225 | 2226 | 2227 | 2228 | 2229 | 2230 | 2231 | 2232 | 2233 | 2234 | 2235 | 2236 | 2237 | 2238 | 2239 |
| 2240 | 2241 | 2242 | 2243 | 2244 | 2245 | 2246 | 2247 | 2248 | 2249 | 2250 | 2251 | 2252 | 2253 | 2254 | 2255 | 2256 | 2257 | 2258 | 2259 |
| 2260 | 2261 | 2262 | 2263 | 2264 | 2265 | 2266 | 2267 | 2268 | 2269 | 2270 | 2271 | 2272 | 2273 | 2274 | 2275 | 2276 | 2277 | 2278 | 2279 |
| ... (same state) ... | |||||||||||||||||||
| 2960 | 2961 | 2962 | 2963 | 2964 | 2965 | 2966 | 2967 | 2968 | 2969 | 2970 | 2971 | 2972 | 2973 | 2974 | 2975 | 2976 | 2977 | 2978 | 2979 |
| 2980 | 2981 | 2982 | 2983 | 2984 | 2985 | 2986 | 2987 | 2988 | 2989 | 2990 | 2991 | 2992 | 2993 | 2994 | 2995 | 2996 | 2997 | 2998 | 2999 |
| 3000 | 3001 | 3002 | 3003 | 3004 | 3005 | 3006 | 3007 | 3008 | 3009 | 3010 | 3011 | 3012 | 3013 | 3014 | 3015 | 3016 | 3017 | 3018 | 3019 |
| 3020 | 3021 | 3022 | 3023 | 3024 | 3025 | 3026 | 3027 | 3028 | 3029 | 3030 | 3031 | 3032 | 3033 | 3034 | 3035 | 3036 | 3037 | 3038 | 3039 |
| ... (same state) ... | |||||||||||||||||||
| 3800 | 3801 | 3802 | 3803 | 3804 | 3805 | 3806 | 3807 | 3808 | 3809 | 3810 | 3811 | 3812 | 3813 | 3814 | 3815 | 3816 | 3817 | 3818 | 3819 |
| 3820 | 3821 | 3822 | 3823 | 3824 | 3825 | 3826 | 3827 | 3828 | 3829 | 3830 | 3831 | 3832 | 3833 | 3834 | 3835 | 3836 | 3837 | 3838 | 3839 |
| 3840 | 3841 | 3842 | 3843 | 3844 | 3845 | 3846 | 3847 | 3848 | 3849 | 3850 | 3851 | 3852 | 3853 | 3854 | 3855 | 3856 | 3857 | 3858 | 3859 |
| ... (same state) ... | |||||||||||||||||||
| 3980 | 3981 | 3982 | 3983 | 3984 | 3985 | 3986 | 3987 | 3988 | 3989 | 3990 | 3991 | 3992 | 3993 | 3994 | 3995 | 3996 | 3997 | 3998 | 3999 |
We have tested all consecutive even numbers up to 4·10^18, and, so far, double-checked our results up to 4·10^17 (in all, 581701 intervals of 10^12 were double-checked). About 781.8 single-core CPU years were used to do all this.
As far as we are aware, the previous record of computation was 4·10^14 [5]. As expected, no counter-example of the conjecture was found. In this table [24KiB, compressed with gzip] we present all values of S(p) we were able to compute, as well as counts of the number of times each (small) prime was used in a minimal Goldbach partition. The record-holders, i.e., numbers larger than all previous ones of the same kind, are clearly marked in the table, which extends the tables 1 and 2 of [4] and table 1 of [5]. The following figure presents a graph with the available values of S(p).
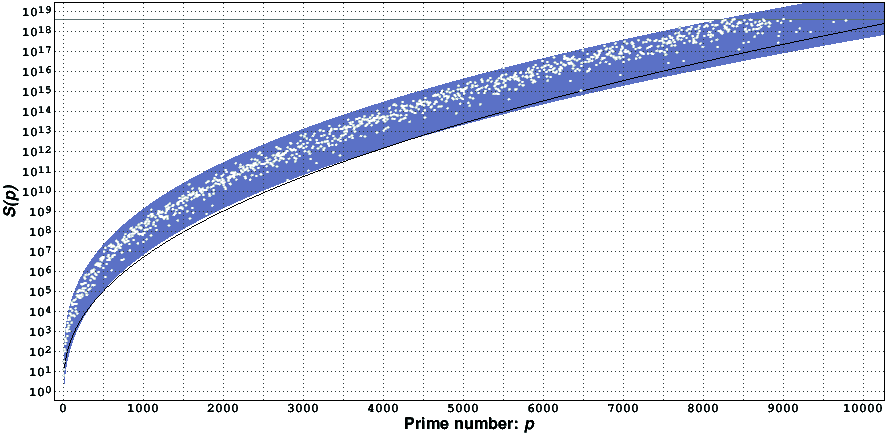
The values of S(p) are bounded, for our empirical data, by the functions
0.4 0.4
0.4 p 0.4 p
S_min(p) = 0.06 p e and S_max(p) = 11.05 p e .
The two kinds of record-holders marked in the table mentioned above correspond to the values of S(p) closer to one of the two bounds. For large p the values of S(p) appear to be slowly approaching the upper bound; hence, the asymptotic growth rate of S(p) probably has a different functional form. In [6] it was stated, based on probabilistic considerations, that p should not grow faster than log^2 S(p) log log S(p). Our data is not enough to resolve this conjecture; the black curve corresponds to the line 1.527 log^2 S(p) log log S(p) (according to the conjecture, all data points should be above the line). It was found that for all our data p can be reasonably well approximated by 0.33(log S(p) log log S(p))^2. In [7] other, probably better, approximations to S(p) are studied in more detail.
Let D(x;p) be the relative frequency of occurrence of the prime p in the minimal Goldbach partition of the even numbers not larger than x. The following figure presents a graph of this function, computed for our current verification limit of the Goldbach conjecture.
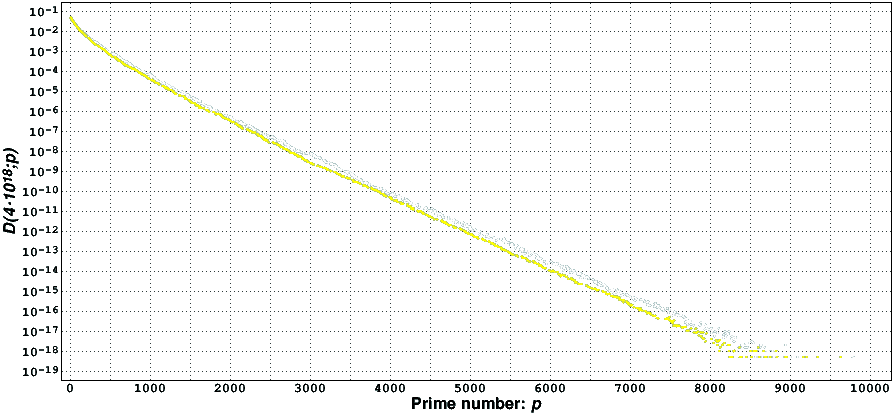
Besides the expected near exponential decay of D(x;p), it is interesting to observe that there exists a distinct difference of behavior in the values of this function when p is a multiple of three plus one (white dots) and when it is not (yellow dots).
Hardy-Littlewood constants
If one assumes the truth of the prime k-tuple conjecture [2], it is possible to estimate the number of occurrences up to x of minimal Goldbach partitions with a smallest prime of p, denoted here by L(x;p), for relatively small values of p [7]. We managed to compute all relevant constants necessary to do this for all (odd primes) p smaller than 250. The constants, and minimal details about how they can be used to estimate L(x;p), can be found here [47KiB, compressed with gzip].
Top 50
The following table presents the 50 largest p (least primes of a Goldbach partition) found so far, with S(p)<4·10^18, either by contributors to this project or by other discoverers (those have an * before the discoverer name). Repeated values of p were excluded from this list.
| Rank | p | S(p) | Discoverer |
|---|---|---|---|
| 1 | 9781 | 3325 58170 73339 60528 | Silvio Pardi |
| 2 | 9629 | 2795 93511 65744 69638 | Silvio Pardi |
| 3 | 9341 | 906 03057 95622 79642 | John Fettig & Nahil Sobh |
| 4 | 9203 | 1348 11357 94295 47486 | Siegfried "Zig" Herzog |
| 5 | 9161 | 887 12380 30778 37868 | Siegfried "Zig" Herzog |
| 6 | 9091 | 3164 06916 06618 44912 | Silvio Pardi |
| 7 | 9001 | 3893 00922 74334 20582 | Tomás Oliveira e Silva |
| 8 | 8971 | 2588 35699 18831 39892 | Tomás Oliveira e Silva |
| 9 | 8951 | 914 47723 42519 16254 | John Fettig & Nahil Sobh |
| 10 | 8941 | 555 27435 15567 50822 | Siegfried "Zig" Herzog |
| 11 | 8933 | 258 54942 69161 49682 | Siegfried "Zig" Herzog |
| 12 | 8929 | 3124 35916 66041 72278 | Silvio Pardi |
| 13 | 8831 | 2408 33984 92355 52478 | Tomás Oliveira e Silva |
| 14 | 8821 | 1670 95614 81435 30128 | Tomás Oliveira e Silva |
| 15 | 8819 | 2717 57304 70073 92768 | Silvio Pardi |
| 16 | 8779 | 2314 72006 67403 14852 | Tomás Oliveira e Silva |
| 17 | 8761 | 3239 05756 38344 11028 | Silvio Pardi |
| 18 | 8747 | 3732 28263 42720 65914 | Tomás Oliveira e Silva |
| 19 | 8737 | 764 63115 78502 42766 | Siegfried "Zig" Herzog |
| 20 | 8731 | 2390 68041 75101 89328 | Tomás Oliveira e Silva |
| 21 | 8719 | 1570 80604 90039 48202 | Tomás Oliveira e Silva |
| 22 | 8707 | 2171 73319 79842 32734 | Siegfried "Zig" Herzog |
| 23 | 8699 | 2994 28857 66127 17268 | Tomás Oliveira e Silva |
| 24 | 8693 | 2046 38924 98824 24466 | Tomás Oliveira e Silva |
| 25 | 8689 | 1302 37600 11943 70768 | Siegfried "Zig" Herzog |
| 26 | 8681 | 771 06523 23704 26528 | Siegfried "Zig" Herzog |
| 27 | 8677 | 1928 32489 01056 96568 | Tomás Oliveira e Silva |
| 28 | 8663 | 1262 36426 84331 28726 | Siegfried "Zig" Herzog |
| 29 | 8647 | 2725 05867 19612 97876 | Silvio Pardi |
| 30 | 8641 | 517 71184 25980 37624 | Tomás Oliveira e Silva |
| 31 | 8629 | 1238 28931 11321 16112 | Siegfried "Zig" Herzog |
| 32 | 8623 | 1211 65003 16991 77606 | Tomás Oliveira e Silva |
| 33 | 8609 | 1872 49629 32659 49398 | Siegfried "Zig" Herzog |
| 34 | 8599 | 3556 57986 77406 73142 | Silvio Pardi |
| 35 | 8597 | 2218 70802 03257 72974 | Siegfried "Zig" Herzog |
| 36 | 8581 | 3663 29859 59299 27532 | Silvio Pardi |
| 37 | 8573 | 1134 05983 29344 00206 | Siegfried "Zig" Herzog |
| 38 | 8563 | 280 46026 69116 44252 | Tomás Oliveira e Silva |
| 39 | 8543 | 2297 37834 24924 06154 | Tomás Oliveira e Silva |
| 40 | 8539 | 941 90839 15563 21548 | Siegfried "Zig" Herzog |
| 41 | 8527 | 1295 15748 05397 26954 | Siegfried "Zig" Herzog |
| 42 | 8521 | 1176 80059 43587 37918 | Siegfried "Zig" Herzog |
| 43 | 8513 | 3431 34334 19613 51016 | Silvio Pardi |
| 44 | 8501 | 255 32912 66885 55994 | Siegfried "Zig" Herzog |
| 45 | 8467 | 2576 43841 05051 31868 | Tomás Oliveira e Silva |
| 46 | 8461 | 2565 58105 68187 05782 | Tomás Oliveira e Silva |
| 47 | 8447 | 2764 13588 98014 80338 | Silvio Pardi |
| 48 | 8443 | 121 00502 23040 07026 | Tomás Oliveira e Silva |
| 49 | 8431 | 2290 65390 58512 00938 | Tomás Oliveira e Silva |
| 50 | 8419 | 1730 12004 22605 42848 | Tomás Oliveira e Silva |
Contributors
The following table presents some details about the contribution of all (past and present) individuals or organizations which donated computing power to this project.
| Name | Location | Number of tasks |
Number of first (known) occurrences | |
|---|---|---|---|---|
| Minimal Goldbach partitions | Prime gaps | |||
| Tomás Oliveira e Silva | All | 2100920 | 325 (0) | 70 (0) |
| DETUA | 1510546 | 191 (0) | 51 (0) | |
| Home | 440316 | 11 (0) | 12 (0) | |
| Kraken | 109000 | 4 (0) | 1 (0) | |
| IEETA | 41058 | 119 (0) | 6 (0) | |
| Siegfried "Zig" Herzog | PSU | 1471605 | 80 (0) | 52 (0) |
| Silvio Pardi | INFN | 869080 | 15 (0) | 9 (0) |
| Christian Kern | Germany | 48999 | 3 (0) | 2 (0) |
| John Fettig & Nahil Sobh | NCSA | 33641 | 2 (0) | 1 (0) |
| João Manuel Rodrigues | DETUA | 16072 | 9 (0) | 2 (0) |
| António Teixeira | IEETA | 14995 | 0 (0) | 1 (0) |
| Carlos Bastos | DETUA | 8646 | 11 (0) | 1 (0) |
| SIAS Group | IEETA | 7752 | 2 (0) | 0 (0) |
| Rui Arnaldo Costa | IEETA | 3847 | 4 (0) | 0 (0) |
| Armando Pinho | IEETA | 3285 | 2 (0) | 1 (0) |
| Miguel Oliveira e Silva | DETUA | 2659 | 7 (0) | 0 (0) |
| Laurent Desnoguès | France | 200 | 0 (0) | 0 (0) |
| All | All | 4581701 | 460 (0) | 139 (0) |
This work was partially supported by the National Center for Supercomputing Applications and utilized the NCSA Xeon cluster.
This research was partially supported by an allocation of advanced computing resources supported by the National Science Foundation. Part of the computations were performed on Kraken (a Cray XT5) at the National Institute for Computational Sciences.
References
| [1] | Richard K. Guy, Unsolved problems in number theory, third edition, Springer-Verlag, 2004. |
| [2] | G. H. Hardy and J. E. Littlewood, Some problems of `partitio numerorum'; III: on the expression of a number as a sum of primes, Acta Mathematica, vol. 44, pp. 1-70, 1922. |
| [3] | Richard Crandall and Carl Pomerance, Prime numbers: a computational perspective, Springer-Verlag, 2001. |
| [4] | Matti K. Sinisalo, Checking the Goldbach conjecture up to 4·10^11, Mathematics of Computation, vol. 61, no. 204, pp. 931-934, October 1993. |
| [5] | Jörg Richstein, Verifying the Goldbach conjecture up to 4·10^14, Mathematics of Computation, vol. 70, no. 236, pp. 1745-1749, July 2000. |
| [6] | A. Granville, J. van de Lune, and H. J. J. te Riele, Checking the Goldbach conjecture on a vector computer, in Number Theory and Applications, R. A. Mollin (ed.), pp. 423-433, Kluwer Academic Press, 1989. |
| [7] | Tomás Oliveira e Silva, Siegfried Herzog, and Silvio Pardi, Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4·10^18, Mathematics of Computation, vol. 83, no. 288, pp. 2033-2060, July 2014 (published electronically on November 18, 2013). |
Additional links
- Our prime gaps page.
- MathWorld's k-tuple conjecture page.
- Cracking Goldbach's Conjecture (European Grid Infrastructure case studies)