Tables of approximate values of the first zeros on
the critical line of some primitive Dirichlet L-series
Introduction
This page presents the results of my efforts to compute the first zeros, on the critical line, of some Dirichlet L-series. Only some L-series associated with Dirichlet characters [1] were considered. The Dirichlet L-series associated with the simplest character is the well-known zeta function. Riemann, in a path-breaking paper [2], conjectured that the non-trivial zeros of this function have real part equal to 1/2 (the critical line). This constitutes the famous Riemann Hypothesis (RH). The Extended Riemann Hypothesis (ERH) asserts the same for all Dirichlet L-series associated with characters.
Although my program is able to compute zeros of Dirichlet L-series without outside help, I used Michael Rubinstein's L-function calculator [3] to compute an initial approximation of the zeros I wanted, which were then refined (to 20 digits after the decimal point) using the PARI/GP calculator.
The character associated to the zeros in each (compressed) file given below is fully described in the header of that file. Only zeros with positive imaginary part are given.
Tables with approximate values of the first zeros of some Dirichlet L-series, last update made on August 7, 2007
Primitive characters:
- The first 10000 zeros of the primitive character [125k, compressed with gzip]
001-000 - The first 10000 zeros of the primitive character [125k, compressed with gzip]
003-001 - The first 10000 zeros of the primitive character [125k, compressed with gzip]
004-001 - The first 10000 zeros of the primitive characters [125k each, compressed with gzip]
005-001 005-002 005-003 - The first 10000 zeros of the primitive characters [125k each, compressed with gzip]
007-001 007-002 007-003 007-004 007-005 - The first 10000 zeros of the primitive characters [125k each, compressed with gzip]
008-001 008-003 - The first 10000 zeros of the primitive characters [125k each, compressed with gzip]
009-001 009-002 009-004 009-005 - The first 10000 zeros of the primitive characters [125k each, compressed with gzip]
011-001 011-002 011-003 011-004 011-005 011-006 011-007 011-008 011-009 - The first 10000 zeros of the primitive character [125k, compressed with gzip]
012-003 - The first 10000 zeros of the primitive characters [125k each, compressed with gzip]
013-001 013-002 013-003 013-004 013-005 013-006 013-007 013-008 013-009 013-010 013-011 - The first 10000 zeros of the primitive characters [124k each, compressed with gzip]
015-001 015-003 015-006 - The first 10000 zeros of the primitive characters [124k each, compressed with gzip]
016-002 016-003 016-006 016-007 - The first 10000 zeros of the primitive characters [124k each, compressed with gzip]
020-001 020-003 020-007 - The first 10000 zeros of the primitive characters [124k each, compressed with gzip]
024-001 024-003 - The first 10000 zeros of the primitive characters [124k each, compressed with gzip]
040-003 040-004 040-005 040-008 040-014 040-015 - The first 10000 zeros of the primitive characters [124k each, compressed with gzip]
060-001 060-004 060-013 - The first 10000 zeros of the primitive characters [124k each, compressed with gzip]
120-004 120-009 120-014 120-016 120-026 120-029
Non-primitive characters:
- The first 10 zeros of the non-primitive character [1k, compressed with gzip]
002-000 - The first 10 zeros of the non-primitive character [1k, compressed with gzip]
003-000 - The first 10 zeros of the non-primitive character [1k, compressed with gzip]
004-000 - The first 10 zeros of the non-primitive character [1k, compressed with gzip]
005-000 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
006-000 006-001 - The first 10 zeros of the non-primitive character [1k, compressed with gzip]
007-000 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
008-000 008-002 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
009-000 009-003 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
010-000 010-001 010-002 010-003 - The first 10 zeros of the non-primitive character [1k, compressed with gzip]
011-000 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
012-000 012-001 012-002 - The first 10 zeros of the non-primitive character [1k, compressed with gzip]
013-000 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
014-000 014-001 014-002 014-003 014-004 014-005 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
015-000 015-002 015-004 015-005 015-007 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
016-000 016-001 016-004 016-005 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
020-000 020-002 020-004 020-005 020-006 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
024-000 024-002 024-004 024-005 024-006 024-007 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
030-000 030-001 030-002 030-003 030-004 030-005 030-006 030-007 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
040-000 040-001 040-002 040-006 040-007 040-009 040-010 040-011 040-012 040-013 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
060-000 060-002 060-003 060-005 060-006 060-007 060-008 060-009 060-010 060-011 060-012 060-014 060-015 - The first 10 zeros of the non-primitive characters [1k each, compressed with gzip]
120-000 120-001 120-002 120-003 120-005 120-006 120-007 120-008 120-010 120-011 120-012 120-013 120-015 120-017 120-018 120-019 120-020 120-021 120-022 120-023 120-024 120-025 120-027 120-028 120-030 120-031
Spectral analysis of the zeros of the zeta function
In 2010, inspired by the pair correlation of the differences between zeta zeros, in particular, by figure 13 of [4], I contemplated the possibility of predicting the location of the zeros of the zeta function (on the critical line) near an interval where all zeros had already been computed. To that end, and to make the predictions potentially more accurate, I worked not with the differences between consecutive zeros but with the differences between the zeros and known reference points.
Let γn be the (positive) imaginary part of the n-th zero of the zeta function on the critical strip; for example, γ1=14.134725.... For the range of values of n that we will be working with, the Riemann Hypothesis is known to be true, so the real part of the zeros will be 1/2. Let Gn be the n-th shifted Gram-point, which satisfies θ(t)=(n-3/2)π where θ(t) is the Riemann-Siegel theta function; for example, G1=14.517919.... Let un=γn-Gn and let vn=θ(γn)/π-(n-3/2); un is the difference between a zero and the corresponding reference point, and vn is the normalized difference. For example, u1=-0.383194... and v1=-0.050252.... Note that un/vn is approximately 2π/log(t/(2π)). The mean value of un, and that of vn, appears to be zero. At large height, that is, for large values of γn, when one is considering a relatively small interval the factor 2π/log(t/(2π)) will be almost constant, and so it will be almost the same to work with un or with vn. We use vn because it implies an average distance between normalized zeros of one.
Figure 13 of [4] suggests that if we compute a Discrete Fourier Transform (DFT) of a finite number of normalized differences of consecutive zeros of the zeta function on the critical line we get what appears to be spectral lines. Replacing the differences between consecutive zeros by the differences between the zeros and our reference points, and doing this for intervals centered at different locations we get the following figure.
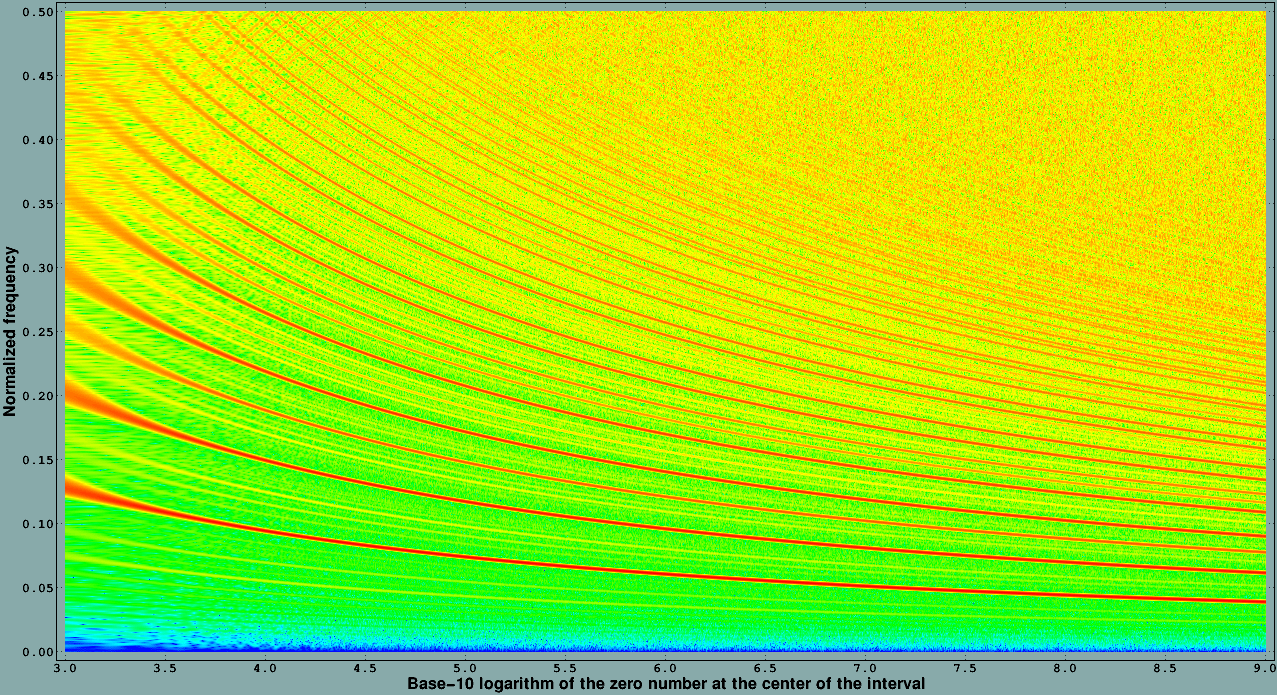
We used 200 intervals per decade, and DFTs with 1281 points (the central point, plus 640 points on each side). Before performing the DFT we applied a Kaiser-Bessel window with α=3.0. This figure suggests that there exists a lot of underlying structure in the way the zeros of the zeta function are located. It even suggests a formula, very likely divergent, for the inverse of the κ(n) function introduced in [5].
Unfortunately, although it is possible to compute with reasonable precision the parameters of the more energetic "spectral lines" based on zero data on a given interval, given the plethora of "spectral lines" observed in the figure, our original goal of predicting the location of the zeros near a given interval turned out to give relatively poor results.
Pérez-Marco phenomenon
In an interesting preprint [6] Ricardo Pérez-Marco uncovered an unexpected anomaly in the distribution of the differences between zeros (not necessarily consecutive) of Dirichlet L-series on the critical line; in the special case of the zeta function, this anomaly was already known [7]. It appears that these differences have a somewhat smaller density when they are close to the imaginary parts of the zeros of the zeta function! Moreover, the differences between zeros of Dirichlet L-series also seem to "avoid" the imaginary parts of the zeta zeros! The following (very wide) figure illustrates what is going on for the zeta zeros. The interval between 0 and 200 was subdivided into 100000 small bins, and the number of differences between the first 10^6, 10^7, 10^8, and 10^9 zeros of the zeta function than fell in each bin was counted; thus, we are estimating the so-called pair correlation of the unscaled zeros. Each of the four curves presents the normalized counts (one corresponds to an uniform density) for the number of zeros given above. To reduce high-frequency fluctuations the data was smoothed using a triangular window and then down-sampled. The gray vertical lines pinpoint the location of the zeta zeros (see also figure 3 of [8]).
As can be seen in the figure, the dips in the density of differences coincide with the zeros of the zeta function. These dips become less pronounced when more zeta zeros are used to form the differences, as explained in [9].
References
| [1] | H. Davenport, Multiplicative number theory, Graduate Texts in Mathematics, Vol. 74, Third Edition, 2000, Springer. |
| [2] | H. M. Edwards, Riemann's zeta function, 2001, Dover Publications, Inc. (first published in 1974 by Academic Press, Inc.). |
| [3] | M. Rubinstein, L-function calculator. |
| [4] | A. M. Odlyzko, On the distribution of spacings between zeros of the zeta function, Mathematics of Computation, vol. 48, no. 177, pp. 273-308, January 1987. |
| [5] | J. Arias de Reyna and J. van de Lune, On the exact location of the non-trivial zeros of Riemann's zeta function, arXiv:1305.3844v2 [math.NT], June 4, 2013. |
| [6] | R. Pérez Marco, Statistics on Riemann zeros, arXiv:1112.0346v1 [math.NT], December 1, 2011. |
| [7] | M. V. Berry and J. P. Keating, The Riemann Zeros and Eigenvalue Asymptotics, SIAM Review, vol. 41, no. 2, pp. 236-266, 1999. |
| [8] | N. C. Snaith, Riemann Zeros and Random Matrix Theory, Milan Journal of Mathematics, vol. 78, no. 1, pp. 135-152, August 2010. |
| [9] | K. Ford and A. Zaharescu, Unnormalized differences between zeros of L-functions, arXiv:1305.2520v3 [math.NT], May 5, 2014. |