Computational verification of the
5x+1 and 7x+1 conjectures
Introduction
Let x be an integer. Let the function T_5(x) be equal to x/2 if x is divisible by 2, equal to x/3 if x is divisible by 3 but not by 2, and equal to 5x+1 otherwise. In a similar way, let the function T_7(x) be equal to x/2 if x is divisible by 2, equal to x/3 if x is divisible by 3 but not by 2, equal to x/5 if x is divisible by 5 but not by 2 and 3, and equal to 7x+1 otherwise. Just like the 3x+1 function (alternative link), it appears that, starting from any positive integer, the repeated iteration of the T_5(x) and T_7(x) functions eventually reach the integer one, after which the iterates enter a cycle. These are the 5x+1 and 7x+1 conjectures. (The 5x+1 conjecture was suggested to me by Eric Roosendaal.)
The two functions defined above are special cases of the generalized 3x+1 mapping proposed by Keith Matthews.
The trajectory of n is the sequence { n, T_p(n), T_p(T_p(n)), ..., T_p^(k)(n), ... }, where T_p^(k)(n) denotes the k-th iterate of T_p(x), p=5,7, for an initial value of n. The maximum excursion of n, denoted by t_p(n), is the maximum value of the trajectory of n, if that number exists, or infinity, otherwise. Furthermore, n is a maximum excursion record-holder if t_p(m)<t_p(n) for all integers m belonging to the interval 1<m<n.
Computational results
In order to test the 5x+1 and 7x+1 conjectures, we wrote two (similar) computer programs (in the programming language C) that compute the trajectories of all interesting initial values of n smaller that a given limit. The large majority of initial values are not interesting, because it can be shown that their iterates reach a value smaller that the initial value is a small number of iterates; the tree pruning method used to identify these initial values is similar to the one used for the 3x+1 function. Both programs were run (for several months) on the spare time of a GNU/Linux 450MHz Pentium III computer.
Using the main ideas of our new 3x+1 (alternative link) verification program, we recently implemented a new version of the 5x+1 verification program; it is about 6 times faster than the original program (measurements made on the same computer).
In the following figure we present the T_5(x) maximum excursion record-holders found [2KiB, compressed with gzip] by the new program, which tested all numbers smaller than 10000002894004224 > 1.000·10^16.
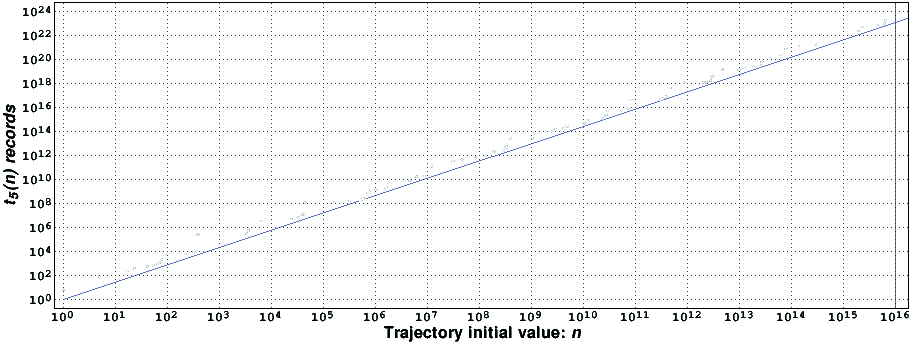
It is remarkable that the t_5(n) records are always close to n^rho5, with rho5=1.442762198279 (straight line in the figure). This value was computed using the ideas of [1], adapted to a Markov chain random walk that mimics the behavior of the T_5(x) function [2].
In the following figure we present the T_7(x) maximum excursion record-holders found [2k, compressed with gzip] by the program, which tested all numbers smaller than 10000000022400000 > 1.000·10^16.
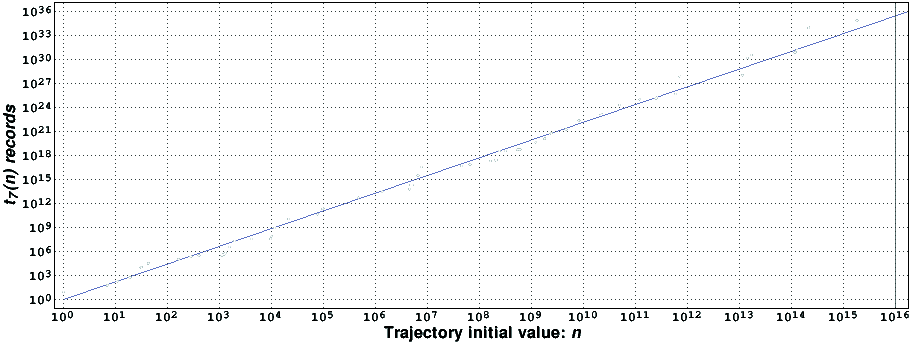
It is also remarkable that the t_7(n) records are always close to n^rho7, with rho7=2.215508001593 (straight line in the figure). Again, this value was computed using the ideas of [1], adapted to a Markov chain random walk that mimics the behavior of the T_7(x) function [2].
References
| [1] | J. C. Lagarias and A. Weiss, The 3x+1 problem: two stochastic models, The Annals of Applied Probability, vol. 2, no. 1, pp. 229-261, 1992. |
| [2] | Tomás Oliveira e Silva, Empirical Verification of the 3x+1 and Related Conjectures. In The Ultimate Challenge: The 3x+1 Problem (book edited by Jeffrey C. Lagarias), pp. 189-207, American Mathematical Society, 2010. |
Additional links
- Our 3x+1 conjecture verification page (alternative link).