Gaps between consecutive primes
Introduction
The computation of the first occurrence of prime gaps of a given (even) size between consecutive primes has some theoretical interest [1, problem A8], [2]. Let p_k be the k-th prime number, i.e., p_1=2, p_2=3, p_3=5, ..., and let g_k=p_(k+1)-p_k be the gap between the consecutive primes p_k and p_(k+1). Harald Cramér [3] conjectured, based on probabilistic ideas, that the large values of g_k grow like (log p_k)^2. Our empirical data does not allow us to discriminate between this growth rate and, for example, (log pi(p_k))^2, where pi(x) is the usual prime counting function (note that pi(p_k)=k). Furthermore, the bounds presented below suggest yet another growth rate, namely, that of the square of the so-called Lambert W function. These growth rates differ by very slowly growing factors (like log log p_k). Much more data is needed to verify empirically which one is closer to the true growth rate.
Let P(g) be the least prime such that P(g)+g is the smallest prime larger than P(g). The values of P(g) are bounded, for our empirical data, by the functions
0.5 0.5
0.5 g 0.5 g
P_min(g) = 0.12 g e and P_max(g) = 30.83 g e .
For large g, there bounds are in accord with a conjecture of Marek Wolf [4].
Computational results
Our prime gap computations are a by-product of our Goldbach conjecture verification effort [5]. We have computed the gaps between all prime numbers smaller than 4·10^18, and, so far, double-checked our results up to 4·10^17 (see the detailed status of this extensive computation). Our results agree with whose presented in [6], [7], [8], and [9]. In this table [14KiB, compressed with gzip] we present the values of P(g) we were able to compute, as well as counts of the number of times each gap occurred. The record-holders, i.e., numbers larger than all previous ones of the same kind, are clearly marked in the table. The following figure presents a graph with the available values of P(g). The black line represents the lower bound for P(g) suggested by Cramér's conjecture.
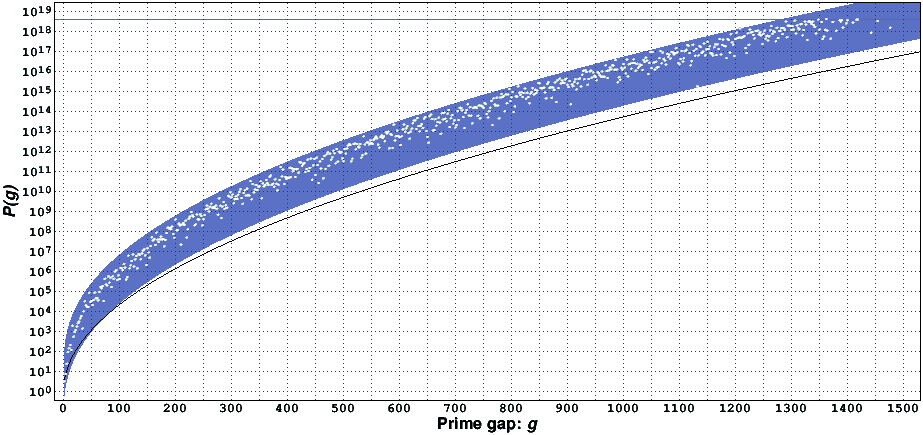
The two kinds of record-holders marked in the table mentioned above correspond to the values of P(g) closer to one of the two bounds presented in the introduction. In this figure it can be seen that the first occurrence of a prime gap of 1132 is abnormally small.
Let D(x;g) be the relative frequency of occurrence of the gap g for all prime numbers not larger than x. The following figure presents a graph of this function, computed for our current verification limit of the Goldbach conjecture.
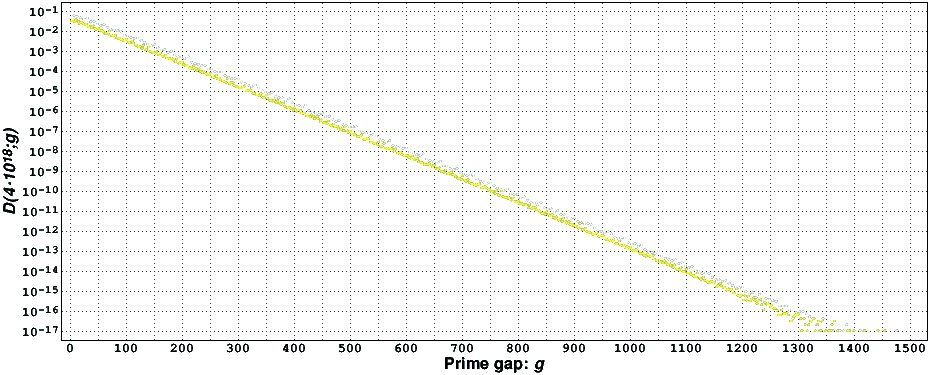
The approximate exponential decay of D(x;g) is explained in [10]. It is visible in this figure that the values of D(x;g) when g is a multiple of 6=2·3 (white dots) are larger than those of their neighbors (yellow dots); those of the multiples of 30=2·3·5, and of 210=2·3·5·7, are even larger.
Hardy-Littlewood constants and jumping champions
If one assumes the truth of the prime k-tuple conjecture [11], it is possible to estimate the number of occurrences up to x of a prime gap of g, denoted here by N(x;g), for relatively small values of g [5], [12]. With the help of Siegfried Herzog we managed to compute all relevant constants necessary to do this for all (even) g smaller than 214. (We double-checked each other's results in full up to g=190 and I checked some of Zig's results for larger values of g.) The constants, and minimal details about how they can be used to estimate N(x;g), can be found here [97KiB, compressed with gzip].
It was observed empirically that these estimates of N(x;g) appear to not deviate from their true values by more that
sqrt(2 N(x;g) log log N(x;g))(law of the iterated logarithm). Using a tolerance 100 times larger than this, our data suggests that:
N(x;6) is larger than N(x;30) for x <= 1.74274357320*10^35
N(x;6) is smaller than N(x;30) for x >= 1.74274357327*10^35
N(x;30) is larger than N(x;210) for
x <= 6.42869106260176003801404998376634178448636748209672
30934734000364513469429976733667048809926190112851
62815790254884411833280961248151172061805903500614
28807728994628470520846144445274265143048582533167
857*10^425
N(x;30) is smaller than N(x;210) for
x >= 6.42869106260176003801404998376634178448636748209672
30934734000364513469429976733667048809926190112851
62815790254884411833280961248151172061805903500614
28807728994628470520846144445274265143048582533167
861*10^25
We expect a change of jumping
champion [10] inside the intervals delimited by these bounds.
Top 50
The following table presents the 50 largest g (prime gaps) found so far, with P(g)<4·10^18, either by contributors to this project or by other discoverers (those have an * before the discoverer name). Repeated values of g were excluded from this list.
| Rank | g | P(g) | Discoverer |
|---|---|---|---|
| 1 | 1476 | 1425 17282 44376 99411 | Tomás Oliveira e Silva |
| 2 | 1454 | 3219 10718 24928 71783 | Silvio Pardi |
| 3 | 1442 | 804 21283 06866 77669 | Siegfried "Zig" Herzog |
| 4 | 1418 | 3725 23553 35041 01511 | Tomás Oliveira e Silva |
| 5 | 1416 | 3750 99252 93399 78877 | Tomás Oliveira e Silva |
| 6 | 1410 | 2635 28193 24815 39903 | Siegfried "Zig" Herzog |
| 7 | 1400 | 3431 65779 58583 78003 | Silvio Pardi |
| 8 | 1398 | 2424 70872 97267 67749 | Tomás Oliveira e Silva |
| 9 | 1392 | 1480 03203 79396 34731 | Tomás Oliveira e Silva |
| 10 | 1390 | 3492 65766 10051 61107 | Silvio Pardi |
| 11 | 1388 | 2975 20552 41233 01149 | Tomás Oliveira e Silva |
| 12 | 1386 | 3449 34008 02746 51527 | Silvio Pardi |
| 13 | 1380 | 1031 50183 31302 43273 | Siegfried "Zig" Herzog |
| 14 | 1374 | 2812 81423 52816 09869 | Silvio Pardi |
| 15 | 1370 | 418 03264 59367 12127 | * D. Knuth |
| 16 | 1364 | 1051 14088 80512 30423 | Siegfried "Zig" Herzog |
| 17 | 1362 | 3937 45795 06462 69397 | Tomás Oliveira e Silva |
| 18 | 1360 | 1153 27764 73035 40597 | Siegfried "Zig" Herzog |
| 19 | 1358 | 523 25522 06146 45319 | Siegfried "Zig" Herzog |
| 20 | 1356 | 401 42992 59991 53707 | * D. Knuth |
| 21 | 1354 | 2805 56288 34484 62853 | Silvio Pardi |
| 22 | 1350 | 1180 35175 22041 37089 | Tomás Oliveira e Silva |
| 23 | 1348 | 3754 93042 77306 28273 | Tomás Oliveira e Silva |
| 24 | 1344 | 753 91763 53808 95597 | Siegfried "Zig" Herzog |
| 25 | 1342 | 1578 16910 61411 87727 | Tomás Oliveira e Silva |
| 26 | 1340 | 1954 31746 71273 10787 | Tomás Oliveira e Silva |
| 27 | 1338 | 2927 64805 72684 73633 | Tomás Oliveira e Silva |
| 28 | 1336 | 2221 89928 82387 68093 | Siegfried "Zig" Herzog |
| 29 | 1334 | 2722 01256 97476 81653 | Silvio Pardi |
| 30 | 1332 | 3103 25146 45367 97599 | Silvio Pardi |
| 31 | 1330 | 2918 47807 68491 34103 | Tomás Oliveira e Silva |
| 32 | 1328 | 352 52122 34513 64323 | Tomás Oliveira e Silva |
| 33 | 1326 | 2075 06944 41432 79153 | Tomás Oliveira e Silva |
| 34 | 1324 | 2937 02084 97138 56977 | Tomás Oliveira e Silva |
| 35 | 1322 | 1106 02843 61874 67937 | Siegfried "Zig" Herzog |
| 36 | 1320 | 605 04633 00290 26447 | Siegfried "Zig" Herzog |
| 37 | 1318 | 2216 27085 98031 42601 | Siegfried "Zig" Herzog |
| 38 | 1316 | 2187 39466 98657 44117 | Siegfried "Zig" Herzog |
| 39 | 1314 | 1214 11964 65476 13277 | Tomás Oliveira e Silva |
| 40 | 1312 | 1396 48771 92534 03577 | Siegfried "Zig" Herzog |
| 41 | 1310 | 1918 58679 96576 17591 | Tomás Oliveira e Silva |
| 42 | 1308 | 749 56545 75543 71299 | Siegfried "Zig" Herzog |
| 43 | 1306 | 3278 01806 91024 80227 | Silvio Pardi |
| 44 | 1304 | 1188 13437 93823 95323 | Tomás Oliveira e Silva |
| 45 | 1302 | 1731 08087 63942 28577 | Tomás Oliveira e Silva |
| 46 | 1300 | 1141 04186 63848 33123 | Siegfried "Zig" Herzog |
| 47 | 1298 | 1739 01802 68170 67239 | Tomás Oliveira e Silva |
| 48 | 1296 | 1799 23519 83799 03447 | Christian Kern |
| 49 | 1294 | 1868 32618 47640 55803 | Siegfried "Zig" Herzog |
| 50 | 1292 | 494 65339 43054 48051 | Tomás Oliveira e Silva |
Contributors
The following table presents some details about the contribution of all (past and present) individuals or organizations which donated computing power to this project.
| Name | Location | Number of tasks |
Number of first (known) occurrences | |
|---|---|---|---|---|
| Minimal Goldbach partitions | Prime gaps | |||
| Tomás Oliveira e Silva | All | 2100920 | 325 (0) | 70 (0) |
| DETUA | 1510546 | 191 (0) | 51 (0) | |
| Home | 440316 | 11 (0) | 12 (0) | |
| Kraken | 109000 | 4 (0) | 1 (0) | |
| IEETA | 41058 | 119 (0) | 6 (0) | |
| Siegfried "Zig" Herzog | PSU | 1471605 | 80 (0) | 52 (0) |
| Silvio Pardi | INFN | 869080 | 15 (0) | 9 (0) |
| Christian Kern | Germany | 48999 | 3 (0) | 2 (0) |
| John Fettig & Nahil Sobh | NCSA | 33641 | 2 (0) | 1 (0) |
| João Manuel Rodrigues | DETUA | 16072 | 9 (0) | 2 (0) |
| António Teixeira | IEETA | 14995 | 0 (0) | 1 (0) |
| Carlos Bastos | DETUA | 8646 | 11 (0) | 1 (0) |
| SIAS Group | IEETA | 7752 | 2 (0) | 0 (0) |
| Rui Arnaldo Costa | IEETA | 3847 | 4 (0) | 0 (0) |
| Armando Pinho | IEETA | 3285 | 2 (0) | 1 (0) |
| Miguel Oliveira e Silva | DETUA | 2659 | 7 (0) | 0 (0) |
| Laurent Desnoguès | France | 200 | 0 (0) | 0 (0) |
| All | All | 4581701 | 460 (0) | 139 (0) |
This work was partially supported by the National Center for Supercomputing Applications and utilized the NCSA Xeon cluster.
This research was partially supported by an allocation of advanced computing resources supported by the National Science Foundation. Part of the computations were performed on Kraken (a Cray XT5) at the National Institute for Computational Sciences.
References
| [1] | Richard K. Guy, Unsolved problems in number theory, third edition, Springer-Verlag, 2004. |
| [2] | Hans Riesel, Prime numbers and computer methods for factorization, second edition, Birkhäuser, 1994. |
| [3] | Harald Cramér, On the order of magnitude of the difference between consecutive prime numbers, Acta Arithmetica, vol. 2, pp. 23-46, 1936. |
| [4] | Marek Wolf, First occurrence of a given gap between consecutive primes, preprint, April 1997. |
| [5] | Tomás Oliveira e Silva, Siegfried Herzog, and Silvio Pardi, Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4·10^18, Mathematics of Computation, vol. 83, no. 288, pp. 2033-2060, July 2014 (published electronically on November 18, 2013). |
| [6] | Jeff Young and Aaron Potler, First occurrence prime gaps, Mathematics of Computation, vol. 52, no. 185, pp. 221-224, January 1989. |
| [7] | Thomas R. Nicely, New maximal prime gaps and first occurrences, Mathematics of Computation, vol. 68, no. 227, pp. 1311-1315, July 1999. |
| [8] | Thomas R. Nicely and Bertil Nyman, First occurrence of a prime gap of 1000 or greater (unpublished). |
| [9] | Bertil Nyman and Thomas R. Nicely, New prime gaps between 10^15 and 5·10^16, Journal of Integer Sequences, vol. 6, no. 3, article 03.3.1, August 2003 (published electronically). |
| [10] | Andrew Odlyzko, Michael Rubinstein, and Marek Wolf, Jumping champions, Experimental Mathematics, vol. 8, no. 2, pp. 107-118, 1999. (For a layman explanation of the results of this paper, see Ian Stewart, Jumping champions, Scientific American, vol. 283, no. 6, pp. 80-81, December 2000.) |
| [11] | G. H. Hardy and J. E. Littlewood, Some problems of `partitio numerorum'; III: on the expression of a number as a sum of primes, Acta Mathematica, vol. 44, pp. 1-70, 1922. |
| [12] | Richard P. Brent, The distribution of small gaps between sucessive primes, Mathematics of Computation, vol. 28, no. 125, pp. 315-324, January 1974. |
Additional links
- Our Goldbach conjecture verification page.
- Our twin prime gaps page.
- MathWorld's k-tuple conjecture page.
- The top-20 prime gaps page.