Gaps between twin primes

Introduction

Let (p,p+2) be a twin prime pair, in which both p and p+2 are prime numbers, and let (q,q+2) be its next twin prime pair, with both q and q+2 also primes and q>p as small as possible. This page presents some data about gaps between twin prime pairs, namely, the number of times a gap of g=q-p appears up to q+2<10^16, denoted by T(g), and the first time, i.e., the smallest value of p, denoted by F(g), that such a gap occurs. Note that g is either 2, which occurs only once, or is a multiple of 6, which occurs an infinite number of times if the prime k-tuples conjecture is true.

Computational results

Using a simple segmented Eratosthenes sieve we computed all gaps between twin prime pairs up to 10^16. In this table [59KiB, compressed with gzip] we present the values of F(g) (first occurrences) and of T(g) (counts) that were observed. The following figure illustrates how T(g) behaves as g increases. The blue dots correspond to gaps that are multiples of 210.

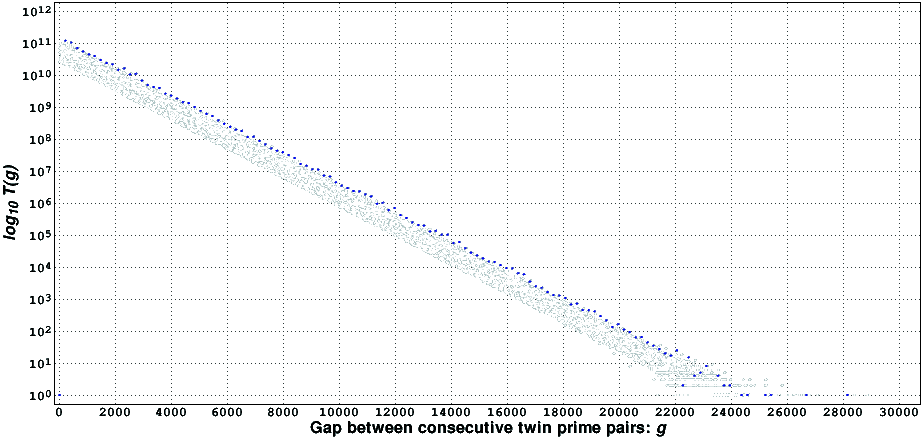
As expected, and like the counts of prime gaps, as g increases we observe an exponential decay in the number of occurrences of gaps of that size. However, the pattern superimposed on top of the exponential decay is more intricate than the one for plain prime gaps.

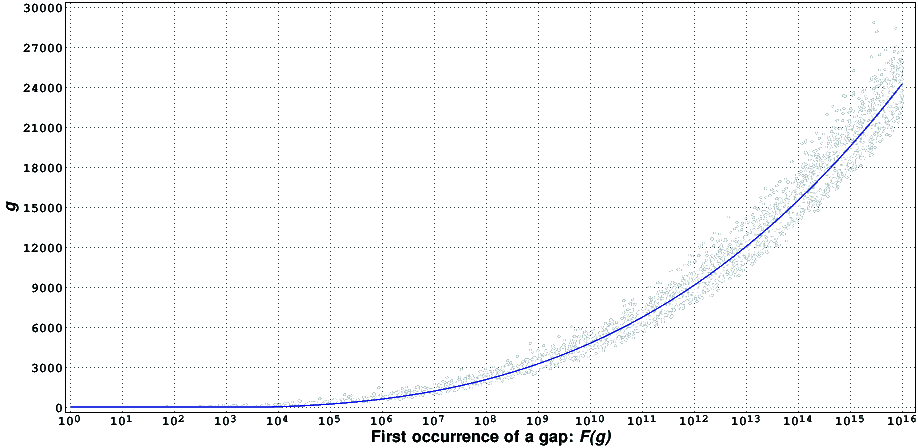
The following figure illustrates how g grows when p increases, by plotting g versus F(g). As suggested in [1], it looks like that g grows like log^3F(g); the blue line corresponds to max(0,0.64log^3F(g)-5.7log^2F(g)).

References