Large fundamental solutions of Pell's equation
Introduction
Let D be a positive integer which is not a perfect square. It is well known that there exist an infinite number of integer solutions to the equation Dx^2+1=y^2, known as Pell's equation. The first non-trivial solution of this Diophantine equation, from which all others can be easily computed, can be found using, e.g., the cyclic method [1], known in India in the 12th century, or using the slightly less efficient but more regular English method [1] (17th century). There are other methods to compute this so-called fundamental solution, some of which based on a continued fraction expansion of the square root of D [2], and some based on more recent ideias [3].
Results (July 16, 2013)
This page describes our attempts to find the values of D that give rise to record-holders in the number of iterations of the cyclic and/or English methods, denoted respectively by nc(D) and ne(D), or in the size of the fundamental solution, denoted by s(D). We define the size of the fundamental solution as the number of base 10 digits of the smallest y larger than one that solves Pell's equation (actually, we use the base 10 logarithm of the fundamental solution). As usual, D is a record-holder for, e.g., the size of the solution, if s(d)<s(D) for all 1<d<D, i.e., the size of the fundamental solution for D is larger than the size of all fundamental solutions for smaller values of D. Although our search was not exhaustive, we are confident that we have not missed any record-holder.
We have tested all interesting values of D up to 10^15. We found empirically that for D>394 all record-holders appear to be congruent, modulo 60, to either 1 or 49. Furthermore, for these values of D all record-holders appear to be prime numbers. We thus restricted our search to the values of D satisfying these conditions. We also found that many small primes tend to be quadratic residues of the record-holders (this is a consequence of the analytic class number formula and the need for a certain Euler product to be large for all record-holder candidates). By Gauss' quadratic reciprocity law, the reverse is also true because the interesting values of D are of the form 4k+1 (it is interesting to note that, modulo 60, the only numbers that are simultaneously quadratic residues modulo 3, 4, and 5 are congruent, modulo 60, to either 1 or 49). This observation allowed us, for large values of D, to restrict the search even more.
The following table present some of the nc(D), ne(D), and s(D) record-holders. The current complete list of record-holders, in an obvious ASCII format, is also available [47KiB, compressed with gzip].
| D | n_c(D) | D | n_e(D) | D | s(D) | ||
|---|---|---|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 2 | 0.477 | ||
| 61 | 14 | 13 | 10 | 61 | 9.247 | ||
| 1549 | 102 | 1201 | 102 | 3061 | 104.051 | ||
| 92821 | 1006 | 56149 | 1010 | 169789 | 1001.282 | ||
| 6810301 | 10266 | 3462229 | 10474 | 12765349 | 10191.729 | ||
| 554156989 | 100060 | 274963789 | 103946 | 1021948981 | 100681.340 | ||
| 47268562069 | 1004162 | 23512531981 | 1011774 | 85489307341 | 1003270.151 | ||
| 4035428570749 | 10025138 | 2022565152661 | 10078082 | 7336466762101 | 10112247.529 | ||
| 366457898547469 | 100105584 | 181637253156109 | 100137522 | 663441817240981 | 100153395.421 | ||
| 993247928289829 | 167921282 | 993247928289829 | 241882218 | 993247928289829 | 124611362.628 |
The following figure presents some of the record-holders, in a log-log graph.
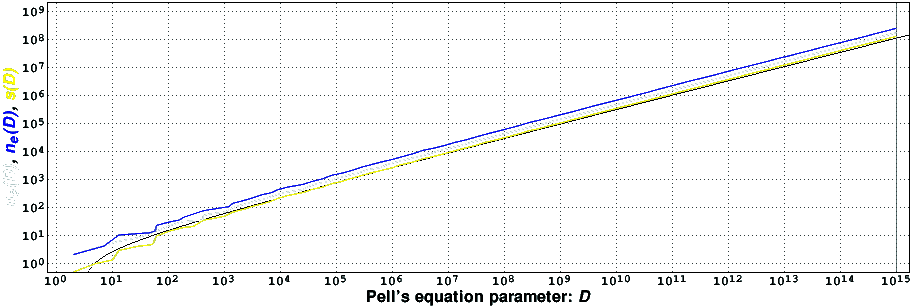
It appears that the record-holders of the functions nc(D) (in white), ne(D) (in blue), and s(D) (in yellow) all grow almost like sqrt(D)log(log(D)) (in black) [4],[5]. In particular, the record-holding values of s(D) are very close to sqrt(D)log(log(D)). Observe, however, that the yellow curve appears to very slowly overtake the black one. That may indicate that the ratio sqrt(D)log(log(D)) / s(D) will converge to a value slightly smaller than one, but it may also indicate that s(D) actually can grow faster than sqrt(D)log(log(D)). Much more empirical data is needed to discriminate between these two cases.
An analysis of all available data also shows that, for large D, the ratio ne(D) / nc(D) appears to converge to a value between 1.440 and 1.441 --- the exact value is probably log(2)/log((1+sqrt(5))/2) --- and that the ratio s(D) / ne(D) appears to converge to a value close to 0.5153. This last value is probably related with the Gauss-Kus'min theorem [6], in which context the number
1 1 log(1+x) pi^2 ------- INTEGRAL -log(x) d -------- = ----------------- = 0.515320417... log(10) 0 log(2) 12 log(2) log(10)
appears more or less naturally.
References
| [1] | Harold M. Edwards, Fermat's last theorem: a genetic introduction to algebraic number theory, Graduate Texts in Mathematics, vol. 50, Springer-Verlag, 1977. |
| [2] | Michael J. Jacobson, Jr., and Hugh C. Williams, Solving the Pell equation, CMS Books in Mathematics, Springer, 2009. |
| [3] | H. W. Lenstra, Jr., Solving the Pell equation, Notices of the AMS, vol. 49, no. 2, pp. 182-192, February 2002. |
| [4] | H. C. Williams, A numerical investigation into the length of the period of the continued fraction expansion of sqrt(D), Mathematics of Computation, vol. 36, no. 154, pp. 593-601, April 1981. |
| [5] | Michael J. Jacobson, Jr., Richard F. Lukes, and Hugh C. Williams, An investigation of bounds for the regulator of quadratic fields, Experimental Mathematics, vol. 4, no. 3, pp. 211-225, 1995. |
| [6] | D. E. Knuth, The art of computer programming. Volume 2: seminumerical algorithms, third edition, Addison-Wesley, 1998. |
Additional links
- MathWorld's Gauss-Kuzmin-Wirsing Constant page.
- CALC has a function to compute the first solution of Pell's equation.