Substituição e instância

Usamos a notação

$\begin{displaymath}s = \left\{ \texttt{X} \leftarrow \texttt{ana},\, \texttt{Z} \leftarrow \texttt{Y}\right\} \end{displaymath}$

para designar uma função s do conjunto das variáveis no conjunto dos termos, que à variável X associa o termo ana, à variável Z associa o termo Y e deixa inalteradas as outras variáveis. Pondo de parte as questões formais da possível confusão entre ``linguagem'' e ``meta-linguagem'', esta função s pode ser definida da maneira habitual: para toda a variável V

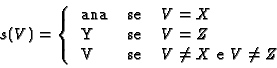
$\begin{displaymath}s(V) = \left\{ \begin{tabular}{lcl} \texttt{ana} & se & $V ... ...$ \\ V & se & $V \ne X$ e $V \ne Z$ \end{tabular} \right. \end{displaymath}$

Dizemos que s é uma substituição. Uma substituição aplica-se, de um modo natural, a termos, átomos ou cláusulas. Por exemplo, se aplicarmos a substituição s à cláusula

         avo(X,Z) :- progenitor(X,Y), progenitor(Y,Z).

obteremos a cláusula

         avo(ana,Y) :- progenitor(ana,Y), progenitor(Y,Y).

A esta cláusula resultante chamamos instância da primeira cláusula pela substituição s. Uma instância por uma substituição, obtém-se substituindo as variáveis pelos termos indicados na substituição. Se $X_1,\, X_2,\, \dots\, X_n$ são as únicas variáveis X para as quais $s(X) \ne X$ e se

$\begin{displaymath}s(X_1)=t_1,\, s(X_2)=t_2,\, \dots\, s(X_n)=t_n \end{displaymath}$

utilizamos a notação

$\begin{displaymath}s = \left\{ X_1 \leftarrow t_1,\,\dots ,\, X_n \leftarrow t_n \right\} \end{displaymath}$

A substituição identidade é denotada por $\left\{\ \right\}$ e deixa inalterada todas as variáveis, e deste modo cada termo, átomo, cláusula, ... A imagem de um termo (átomo, cláusula) por uma substituição é chamada instância do termo (átomo, cláusula) pela substituição. Note-se que uma instância de uma instância de t é uma instância de t. Mais formalmente, a composição de duas substituições, como uma função sobre o conjunto dos termos (átomos, cláusulas) é ainda uma substituição. Estas noções permitem dar um sentido rigoroso à noção de questão e resposta. Seja P um programa e A um átomo. Uma resposta lógica (segundo P) à questão

         ?- A.

é uma substituição s tal que s(A), instância de A por s, é uma consequência lógica de P, quer dizer, $s(\texttt{A}) \in \textit{CL(P)}$ . Segue-se um exemplo para o nosso problema 1: à questão

         ?- avo(rosa,N).

uma das respostas lógicas, de acordo com o programa que fizemos, é

$\begin{displaymath}\left\{ N \leftarrow ana \right\} \end{displaymath}$

Delfim F. Marado Torres
1999-03-16