teorema do limite central
TLC = Teorema do Limite Central
O TLC tem interesse prático especial porque se aplica a uma população caracterizada por uma v.a. com distribuição genérica, ou outra desde que não seja a distribuição normal.
Se X é uma v.a. com média populacional (\mu) e variância populacional (\sigma^2) finitas, então
A média de variáveis aleatórias iid tem um resultado equivalente:
isto é, a média amostral aleatória é caracterizada, de forma aproximada, por uma distribuição normal mesmo que as v.a. X_i não o sejam.
A ter em conta:
se a v.a. é discreta, e apenas nessa condição, pode ser útil fazer a «correção à continuidade»: quando realizar correção à continuidade;
há dois casos particulares de aplicação: TLC e a distribuição de Poisson e TLC e a distribuição binomial.
aplicar o TLC
A expressão «aplicar o TLC» que dizer podemos usar uma distribuição normal para calcular probabilidades e quantis, de forma aproximada, para uma soma de v.a. ou uma média de v.a. se o número n é elevado. Aplicar o TLC resume-se a
caracterizar uma população por uma v.a. X modelada por uma distribuição que não seja a normal;
conhecer a média, \mu, da v.a. X;
conhecer a variância, \sigma^2, da v.a. X;
garantir uma boa aproximação com n \ge 30 (sendo este valor apenas uma referência não obrigatória pois depende da aplicação concreta do TLC);
calcular probabilidades ou quantis usando um dos casos:
Os resultados de probabilidade ou quantis são aproximados e, por isso, também deve ser consultada a próxima secção no caso da v.a. ser discreta.
quando realizar correção à continuidade
O TLC aplica-se a v.a. contínua e, também, a v.a. discreta.
No modelo contínuo, P(X=a)=0, isto é, não há área por baixo do ponto e assim acontece na distribuição normal. Veja a razão aqui.
Porém, no modelo discreto P(X=a)\neq a para valores inteiros a de interesse. Uma soma de v.a. discretas, X_i,
é, ainda, uma v.a. discreta, Y. Aplicando o TLC:
O problema surge porque:
P(Y=a) \neq 0 para a um inteiro de interesse mas
P(Y=a) = 0 se usarmos que Y \sim_{aprox} normal
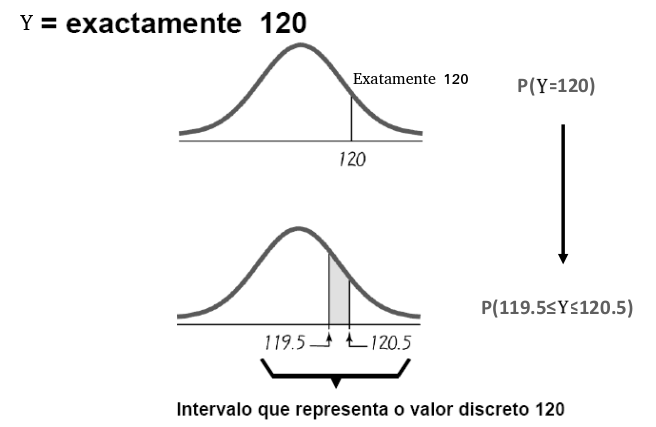
e a solução é fazer a «correção à continuidade»:
P(Y=a) \approx P(a-0.5 \le Y \le a+0.5) sempre que se passa a usar a distribuição normal
sendo um exemplo
P(Y=10) \approx P(9.5 \le Y \le 10.5), ao usar a distribuição normal
Só deve ser feita correção à continuidade quando a v.a. é discreta.
São apresentados dois casos: correção à continuidade da soma ou correção à continuidade da média
correção à continuidade da soma
Se a v.a. é discreta, e apenas nessa condição, pode ser útil fazer a «correção à continuidade da soma» pois
e, pelo TLC, Y \sim_{aprox} Normal(n\,\mu_X, n\,\sigma^2_X) sendo esta aproximação com melhor qualidade se n\ge 30.
O TLC proporciona um valor de probabilidade aproximado. Porém, quando se trata de uma v.a. discreta então ainda se sugere fazer uma segunda correção designada por correção à continuidade que se passa a apresentar. Usando uma expressão, não rigorosa mas intuitiva, em que a é um número inteiro,
em que:
P(Y=a) é a probabilidade caso se conheça a distribuição discreta exata de Y;
P(a-0.5 \le Y \le a+0.5) é a probabilidade obtida como se Y fosse uma v.a. contínua com Y \sim_{aprox} N(n\mu,\; n\sigma^2).
Em resumo:
se queremos Y=a devemos considerar o intervalo a-0.5 \le Y \le a+0.5 (a usar em expressões como Y\le a ou Y\ge a;
se não queremos Y=a, isto é, Y<a ou Y>a, então devemos excluir o intervalo [a-0.5,a+0.5].

correção à continuidade da média
Se a v.a. é discreta, e apenas nessa condição, pode ser útil fazer a «correção à continuidade da média» pois uma média baseia-se numa soma. Veja a secção anterior.
As expressões para a média, \bar X, são:
alternativa
Pode ser mais intuitivo passar à soma:
mas, neste caso, tem que se usar Y \sim_{aprox} N(n\mu,\; n\sigma^2).
TLC e a distribuição de Poisson
Resumo: se X \sim Poisson(\lambda_X), e \lambda_X \ge 5, então X \sim_{aprox} Normal(\lambda_X, \lambda_X).
Um caso particular do TLC aplica-se à distribuição de Poisson. Uma das propriedades da Poisson é que a soma de v.a. de Poisson é ainda modelada por uma Poisson. Se
e cada X_i segue uma Poisson, X_i \sim Poisson(\lambda_X), então Y também segue uma Poisson:
Por outro lado, como a soma de v.a. tem distribuição aproximada a uma distribuição normal:
sendo este resultado uma boa aproximação se n\,\lambda_X \ge 5.
Um resultado apenas para uma v.a. também é válido se
e \lambda_X \ge 5 então
pois podemos ver X como sendo uma soma de n v.a. com média \frac{1}{n} \lambda_X.
TLC e a distribuição binomial
Resumo do conceito: se X \sim binomial(n,\;p), n \ge 30, então X \sim_{aprox} Normal(np,\; np(1-p)).
ou, como se fazia antigamente, «número de sucessos» é na realidade somar v.a. cujos valores são 0 e 1, i.e., 0+1+1+0+1+1 etc = nr de sucessos.
Importante: sempre que há uma soma de muitas v.a. pode-se aplicar o TLC que diz que a distribuição será aproximadamente Normal.
Uma distribuição binomial, por definição, caracteriza uma soma de v.a. Y=X1+…+Xn do seguinte modo: cada Xi pode tomar o valor 1 (no caso de «sucesso») ou tomar o valor 0 (no caso de «insucesso»). Assim, Y é uma soma de v.a. e, sendo uma soma, a sua distribuição aproxima-se à de uma Normal, que é o resultado dado pelo TLC para a soma de v.a..
Em detalhe, como a v.a. Y é binomial então
E[Y] = np
Var[Y] = np(1-p)
e assim, Y \sim_\text{aprox} Normal( np, np(1-p) ).
No caso da binomial, a aproximação tem pouco erro quando np \ge 5 e np(1-p) \ge 5. Sendo Y uma v.a. discreta, pode-se realizar correção à continuidade.
porque é importante
Na investigação de um processo recorrendo a estatística é frequente caracterizar uma população, enquanto modelo matemático, pela sua média populacional (\mu).
Três pontos de vista, cada vez mais gerais:
O TLC estabelece uma relação entre a «média de uma amostra» e a «média populacional» que é um parâmetro de um modelo matemático.
O TLC estabelece uma relação entre amostra e população.
O TLC estabelece uma relação entre a realidade e um modelo matemático.
O modo com é feito está expresso nas expressões acima, no texto.
conceitos e ideia
Conceitos de estatística descritiva envolvidos no TLC:
amostra: colecionam-se várias amostras de dimensão n;
média amostral: calcula-se a média \bar x para cada amostra (teremos várias médias);
histograma: faz-se um histograma com as várias médias «\bar x».
O que se obtém, se usarmos muitas amostras, é um histograma de médias, \bar x, que se aproxima a uma distribuição normal:
Uma imagem mil palavras
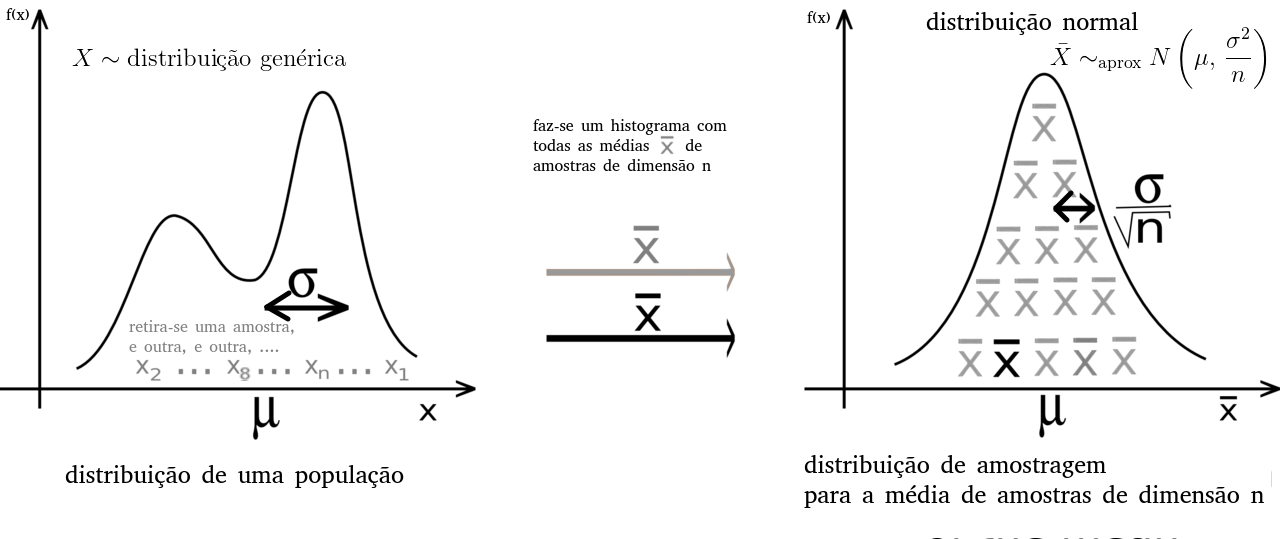
Adaptado de imagem na wikipedia. Mathieu ROUAUD - Own work, CC BY-SA 4.0
exemplo das pintas de um dado de seis faces
Este exemplo é fácil reproduzir em casa.
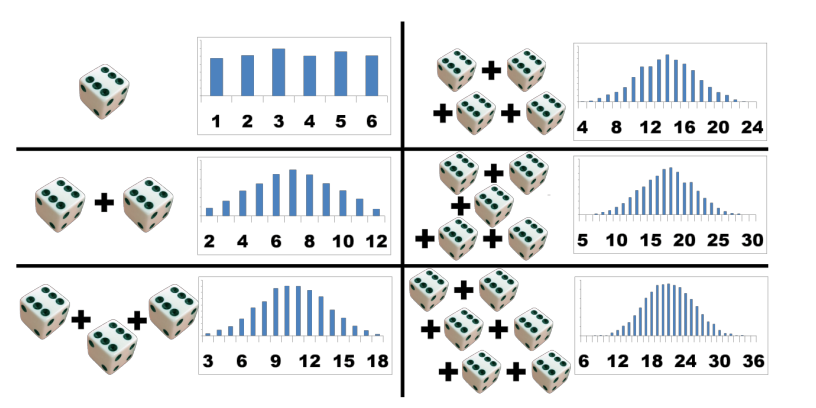
Lançamento de um dado:
o dado é lançado 100 vezes e registados os números obtidos;
obtém-se uma distribuição quase uniforme (probabilidades quase idênticas para os valores 1 a 6);
os resultados de 1, 2, …, 6 são (quase) equiprováveis.
Lançamento de dois dados:
os dois dados são lançados 100 vezes e é registada a soma dos números obtidos;
obtém-se uma distribuição em forma de telhado.
os resultados de 2 (=1+1) e 12 (=6+6) são menos provaveis enquanto que o valor 7 pode ser obtido de seis maneiras (1+6,2+5,3+4,4+3,5+2,6+1) tornando o 7 muito frequente.
Lançamento de três dados:
os três dados são lançados 100 vezes e é registada a soma dos números obtidos;
obtém-se uma distribuição em forma de telhado, já arredondado.
os resultados de 3 (=1+1+1) e 18 (=6+6+6) são menos provaveis enquanto que os valores 10 ou 11 podem ser obtido de muitas maneiras e por isso muito mais prováveis.
etc
Lançamento de seis dados:
os seis dados são lançados 100 vezes e é registada a soma dos números obtidos;
obtém-se uma distribuição já em forma de gaussiana.
o mesmo argumento das situações anteriores sendo que o resultado 6 (=1+1+1+1+1+1) e o resultado 36 (=6+6+6+6+6+6) são pouco prováveis pois só podem ser obtidos desta maneira.