Problema de Dezembro de 2004: Brick Wall Patterns

Este mês apresento um problema mais fácil que os dois anteriores. Apareceu também numa prova local da Universidade do Porto. A solução é muito simples!

If we want to build a brick wall out of the usual size of brick which has a length twice as long as its height, and if our wall is to be two units tall, we can make our wall in a number of patterns, depending on how long we want it. From the figure one observe that:

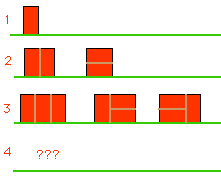
• There is just one wall pattern which is 1 unit wide - made by putting the brick on its end.
• There are 2 patterns for a wall of length 2: two side-ways bricks laid on top of each other and two bricks long-ways up put next to each other.
• There are three patterns for walls of length 3.

1
2
3
0

1
2
3

#include <stdio.h>

int f(int n)
{
	if (n == 0 || n == 1)
		return 1;
	else
		return f(n-1) + f(n-2);
}

int main()
{
	int n;
	
	for (;;) {
		scanf("%d", &n);

		if (n == 0)
			break;

		printf("%d\n", f(n));
	}
	return 0;
}

As soluções geradas estão correctas, mas o programa demora um bocado a calcular f(40). Se o input de teste tiver 1000 linhas com 40 (e isso é bem possível, para testar a rapidez do algoritmo) então o programa vai demorar demasiado tempo e não será aceite.

Porque é que demora tanto tempo a calcular f(40)? Vamos ver primeiro como é calculado f(4). f(4) é decomposto em f(3) + f(2); a função f já foi chamada 3 vezes. f(2) é decomposto em f(1) + f(0) e termina; f foi chamada 5 vezes. Mas ainda falta decompor o f(3) chamado ao início... este decompõe-se em f(2) + f(1), e vamos em 7 chamadas. f(2) ainda se decompõe mais duas vezes e temos no total 9 chamadas da função f. Para calcular f(6) vamos calcular f(5) (que se decompõe em f(4) e por isso tem de repetir estas chamadas todas, mais f(3)) e ainda f(4) outra vez! O crescimento do número de chamadas é exponencial. Para f(40) o total de chamadas é 331160281! Impressionante não :)

Agora que já descobrimos porque demora tanto, será que há uma maneira mais rápida de fazer estas contas? Claro que sim não é... a técnica chama-se dynamic programming e consiste em trocar espaço por tempo para reduzir a complexidade de um algoritmo de exponencial para polinomial. O que é que isto quer dizer? Que podemos criar uma solução que vai usar mais memória (para armazenar resultados intermédios e evitar repetição de cálculos para demorar menos tempo. Nem sempre é possível usar esta técnica; isto só é possível quando as soluções do problema podem ser rapidamente calculadas a partir de soluções anteriores.

Neste caso, existem montes de repetições; para calcular f(6) usamos f(5) e f(4), mas f(5) também usa f(4). É aqui que surge a repetição que vamos evitar. Para isso, vamos armazenar a solução de f(4) num array e quando precisarmos já lá está. Podemos fazer ainda melhor; podemos calcular todas as soluções muito rapidamente e guardá-las na memória. Basta lembrar que f(n) = f(n-1) + f(n-2). Vamos ter um array solution[n] com o valor da solução para n bricks. Se já tivermos solution[3] e solution[4], podemos fazer solution[5] = solution[4] + solution[3]. Agora já temos também solution[5], e podemos fazer solution[6] = solution[5] + solution[4]. E sempre assim até 40... simples :)

Implementação (em C):

#include <stdio.h>

int solution[41];

int main()
{
	int n;

	solution[0] = 1;
	solution[1] = 1;
	
	for (n = 2; n <= 40; n++)
		solution[n] = solution[n-1] + solution[n-2];
	
	for (;;) {
		scanf("%d", &n);

		if (n == 0)
			break;

		printf("%d\n", solution[n]);
	}
	return 0;
}

Iniciamos com as soluções base solution[0] = 1 e solution[1] = 1, e usamos um ciclo for para calcular todas as outras até 40. Repare-se que o ciclo principal do programa apenas lê o valor de n da entrada, e escreve na saída um valor do array; isto é muito muito rápido. No caso de ter 1000 vezes o valor 40 na entrada, isto rapidamente produz 1000 vezes a mesma resposta, sem repetir cálculos.

Nestas situações também é possível fazer código "manhoso", ou seja, em vez de criar uma solução à maneira, usamos um programa mais ou menos lento para calcular todas as soluções, e depois fazemos outro programa com as soluções "inline". Qualquer coisa do género:

#include <stdio.h>

int solution[] = {
	1,
	1,
	2,
	3,
	5,
	8,
	...
	...
	165580141
};

int main()
{
	int n;

	for (;;) {
		scanf("%d", &n);

		if (n == 0)
			break;

		printf("%d\n", solution[n]);
	}
	return 0;
}

Isto pode não resultar se o programa demorar demasiado tempo a gerar as soluções, mas serve bem para safar se não conseguirmos descobrir um algoritmo melhor.

Caso não tenham reparado, a sequência gerada foi a sequência de Fibonacci e é um exemplo comum e simples de dynamic programming. A técnica de pré-calcular todas as respostas pode ser usada muitas vezes, por isso convém ler com atenção os enunciados dos problemas e ver quais são todos os inputs possíveis. Se forem só 40, como neste caso, podemos até criar as tabelas inline. Se o input for, por exemplo, um par de coordenadas (x,y) com x e y no intervalo [0, 100] (valores inteiros), então há 100x100 = 10000 inputs diferentes e também podemos armazenar todas as respostas. Outros problemas, como este, têm inputs que não se podem prever e já não podemos pré-calcular todas as respostas. Para praticar, passo a propôr um problema que se resolve com uma técnica semelhante.