How sandpiles spill: Sandpile problem in a thick flow regime, S.N. Dorogovtsev and J.F.F Mendes
(Phys. Rev. Lett; 83, 2946 (1999)

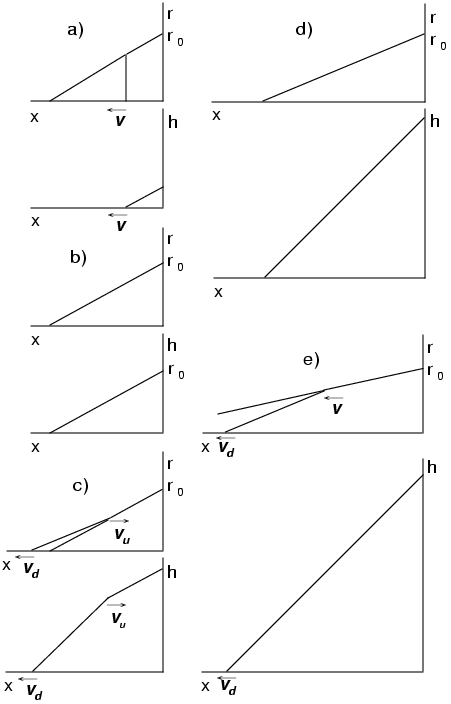
We obtain an analytical solution of a one-dimensional sandpile problem in a thick flow regime when it can be formulated in terms of linear equations. It is shown that a space periodicity takes place during the sandpile evolution even for a sandpile of only one type of particles. Similar periodicity was observed previo usly for many component sandpiles. Space periods are proportional to an input flow of particles $r_0$. We find that the surface angle $\theta$ of the pile reaches it's final critical value ($\theta_f$) from lower values only at long times. The deviation ($\theta_f - \theta$) behaves as $(t/r_{0})^{-1/2}$.

Crossover behaviour of small-world networks, S.N. Dorogovtsev and J.F.F Mendes
(Europhys. Lett; xxx (2000)

We present an exact description of a crossover between two different regimes of simple analogies of small-world networks. Each of the sites chosen with a probability $p$ from $n$ sites of an ordered system defined on a circle is connected to all other sites selected in such a way. Every link is of a unit length. Thus, while $p$ changes from 0 to 1, an averaged shortest distance between a pair of sites changes from $\bar{\ell} \sim n$ to $\bar{\ell} = 1$. We find the distribution of the shortest distances $P(\ell)$ and obtain a scaling form of $\bar{\ell}(p,n)$. In spite of the simplicity of the models under consideration, the results appear to be surprisingly close to those obtained numerically for usual small-world networks.

Language as an evolving word web
S.N. Dorogovtsevand J.F.F Mendes
Proc. Royal Soc. London B 268, 2603-2606 (2001) (2000)

Human language can be described as a complex network of linked words. In such a treatment, each distinct word in language is a vertex of this web, and neighboring words in sentences are connected by edges. It was recently found (Ferrer and Sol\'e) that the distribution of the numbers of connections of words in such a network is of a peculiar form which includes two pronounced power-law regions. Here we treat language as a self-organizing network of interacting words. In the framework of this concept, we completely describe the observed Word Web structure without fitting.

Evolving Networks
S.N. Dorogovtsevand J.F.F Mendes
Advances in Physics, June (2002) (2000)

We review the recent fast progress in statistical physics of evolving networks. Interest has focused mainly on the structural properties of random complex networks in communications, biology, social sciences and economics. A number of giant artificial networks of such a kind came into existence recently. This opens a wide field for the study of their topology, evolution, and complex processes occurring in them. Such networks possess a rich set of scaling properties. A number of them are scale-free and show striking resilience against random breakdowns. In spite of large sizes of these networks, the distances between most their vertices are short --- a feature known as the ``small-world'' effect. We discuss how growing networks self-organize into scale-free structures and the role of the mechanism of preferential linking. We consider the topological and structural properties of evolving networks, and percolation in these networks. We present a number of models demonstrating the main features of evolving networks and discuss current approaches for their simulation and analytical study. Applications of the general results to particular networks in Nature are discussed. We demonstrate the generic connections of the network growth processes with the general problems of non-equilibrium physics, econophysics, evolutionary biology, etc.